《剑指Offer》第2章笔记 数组

数据结构是技术面的重点，主要围绕数组、字符串、链表、树、栈以及队列这几种常见的数据结构展开。

嗯，除了语言和算法以外的最重要的（废话）。

---

数组的一些特点（主要是指C/C++中的基础数组类型）：

• 连续的内存，按照顺序存储；
• 创建时需要指定数组的容量大小；
• O(1)时间读/写任何位置元素；

为了解决基础数组空间效率不高的问题，人们设计了动态数组，比如 C++ STL 中的 vector ，其中为了避免空间浪费，先为数组开辟小空间，当数据数目超过容量时，再重新分配一块更大的空间，把之间的数据复制到新的数组中，再把之前的内存释放（一般没有延续之前地址往后申请内存的操作，所以只能整块申请，然后再释放掉新的），但是这样就会带来内存空间申请和数据迁移的时间开销，因此使用动态数组要尽量减少改变数组容量大小的操作。

在C/C++中，数组和指针既相互关联又有区别。

声明一个数组时，数组的名字也是一个指针（不可修改的指针变量），该指针指向数组的第一个元素。需要注意的是，C/C++不会主动记录数组的大小，所以在访问数组元素时，程序要确保不会超过边界。

int get_size(int data[]) {
  return sizeof(data);
}Error: Cannot find module 'gulplog'

int main() {
  int data1[] = {1, 2, 3, 4, 5};
  int size1 = sizeof(data1);

  int* data2 = data1;
  int size2 = sizeof(data2);

  int size3 = get_size(data1);

  printf("%d, %d, %d", size1, size2, size3);
  // 20, 4, 4
}

在上面的代码中：

• sizeof(data1) == 20：sizeof(data1)求数组的大小（字节数），data1包含5个整数，每个整数4字节，所以20字节；
• sizeof(data2) == 4：data2声明是指针，尽管指向了数组指针，但本质仍然是指针，在32位系统上，对任意指针求sizeof都是4(32位系统是4个字节的地址)；
• get_size(data1) == 4：在C/C++中，数组作为函数参数传递时，会退化为同类型的指针，尽管函数声明的是数组参数，但还是会退化为指针（语言概念特色），所以结果仍然是4。

---

面试题3 题目一：找出数组中重复的数字。

数组长度n，数字都在 0 - n-1 的范围内，数组中某些数字重复，但不知道有几个数字重复，请找出数组中任意一个重复数字；例如{2, 3, 1, 0, 2, 5, 3}，重复数字2或者3。

• 思路1：简单的排序再搜索就可以，但需要 O(nlogn) 的时间开销；
• 改进思路2：常用的一种优化思路是使用哈希表，从头到尾记录所有数字的出现次数，如果次数大于2就是重复的数字，时间开销降低到了 O(n) ，但凭空多了哈希表的 O(n) 开销；

大部分的人都能想到第二种方法，然后书的作者会介绍第三种方法：

数字都在0~n-1的范围内，如果数组不重复，则数字i出现在下标i的位置，如果重复，则某些位置有多个数字，同时有些位置没有数字。

但我觉得对这种方法的阐述，稍微有点凭空跳脱，没有和之前提到的前两种思路有任何延续，所以一时可能较于难以理解这里的思路，尤其是之后的算法流程。

我们可以延续之前的改进思路2，使用哈希表的优点是时间开销少，缺点是多了空间开销，那么进一步的优化思路是：如何减少空间上的开销？

在已知数字出现在 0 ~ n-1 范围内时，哈希表的一种简单实现是位置i存储数字i的出现频率：

int array[5] = {1, 3, 3, 0, 2};
int hash[5] = {0, 0, 0, 0, 0};
... // for num in array to finish hash
cout << hash << endl; // [1, 1, 1, 2, 0]

那么，你可以想到的一种优化思路是：原数组存储的数字在读取过一次后其实就没有作用了，所以在数字i被读取了之后，将它“自己的位置”作为哈希表的存储位，不就不需要额外的空间了么？

更加细节地，在数字i被读取了过后，尽管它本身可能不在位置i上，可以把原本位置i的数字替换到当前的位置，最后我们使用位置i作为数字i的哈希表存储位，就完成了一步操作；对全数组的数字都执行这样的操作，就可以找出重复的数字了。

这个方法本质上是延续哈希表的思路，并且具体实现的方式你就会发现和作者提出的方法是一致的，所以我猜测作者的实质本意是将改进思路2的一种延续优化，但并没有在书中进行说明这种思路转变，稍微有点儿可惜。

PS：这样的改进思路在延续了简单哈希表实现的同时，也延续了这样的哈希表缺点，即无法处理0 ~ n-1 范围以外的数字情况。

从头到尾依次扫描数组中的每个数字，当扫描到位置i的数字m时，判断m==i：

• 如果相等，说明数字i在位置i上，继续执行；
• 如果不相等，将位置m上的数字交换到位置i上，位置m上放置了数字m，从位置i继续下一步判断；如果在交换之前发现，位置m上已经是数字m了，那么就说明数字m重复了，程序结束。

一个栗子：

[1, 3, 3, 0, 2] // i=0
[3, 1, 3, 0, 2] // i=0 1 on 1
[0, 1, 3, 3, 2] // i=0 3 on 3
[0, 1, 3, 3, 2] // i=0 0 on 0
[0, 1, 3, 3, 2] // i=1 1 on 1
[0, 1, 2, 3, 3] // i=2 2 on 2
[0, 1, 2, 3, 3] // i=3 3 on 3
[0, 1, 2, 3, 3] // i=4 3 already on 3, 3 repeat

完整代码实现：

#include <iostream>

int find_repeat(int array[], int len) {
    int i = 0;
    while(i < len) {
        int m = array[i];
        if(m != i) {
            if(array[m] != m) {
                // swap
                int temp = array[m];
                array[m] = m;
                array[i] = temp;
            } else {
                return m;
            }
        } else {
            i++;
        }
    }
    return len;
}

int main() {
    int array[] = {1, 3, 3, 0, 2};
    int len = sizeof(array) / sizeof(array[0]);
    int dup = find_repeat(array, len);
    if(dup == len) {
        printf("No Repeat Number\n");
    } else {
        printf("Repeat Number: %d\n", dup);
    }
    return 0;
}

在其中还可以加上前一节提到的安全、边界等问题的考虑，在下面贴的作者的实现里面可以看到：

bool duplicate(int array[], int len, int* dup) {
    // 考虑参数失效
    if(array == nullptr || len <= 0) {
        return false;
    }
    // 考虑超过边界
    for(int i = 0; i < len; i++) {
        if(array[i] < 0 || array[i] > len - 1) {
            return false;
        }
    }
    // 实现比较优雅 流程相同
    for(int i = 0; i < len; i++) {
        while(array[i] != i) {
            if(array[i] == array[array[i]]) {
                *dup = array[i];
                return true;
            }
            // swap
                int temp = array[i];
                array[i] = array[temp];
                array[temp] = temp;
        }
    }
    return false;
}

---

面试题3 题目二：不修改数组找出重复的数字。

在长度n+1的数组里的所有数字都在1~n的范围内，所以数组至少有一个数字是重复的。请找出数组中任意一个重复的数字，但不能修改输入的数组。

这一题虽然可以像题目一那样，只需要多开辟一个n+1长度的辅助数组，用来解决问题，但是这样就多了O(n)的空间开销。

一般在这种限定情况下，很难再和题目一一样做到时间、空间开销非常小的情况下完成任务，所以可以退一步，不需要缩减到O(n)时间，比如维持和快排复杂度O(nlogn)相同情况下，达成O(1)的空间开销也是一种优化的思路。

因为出发点不同，我们再次退回到最简单的方法：

• 没有额外的空间帮助记录时，就只能每次判断一个数字是否有重复，即判断n次，每次有n长度的遍历开销，也就是O(n^2)；

所以有两个优化的方向：（1）减少判断的次数n；（2）减少遍历长度n。

在没有额外信息辅助的情况下，优化（2）一般是很难做的（因为每个数只有遍历了全部才知道是否有重复），所以我们可以尝试优化（1）的部分。

最简单思路下，只有遍历了1~n的n个数在数组中的情况，才能知道谁重复了，我们可以用一些技巧来减少需要判断的次数。

其实非常巧妙，这条技巧就在题目中：“1~n范围内的数，在长度n+1的数组中必然存在一个重复”，这个命题成立的原因是，如果你遍历一次数组，统计1~n范围内数字的出现次数(n+1)，出现情况是大于n的（这里的n指1~n的这个范围长度），进一步地推广到一个普适命题“i~j范围内的数，在长度n+1的数组中，如果出现次数大于(j-i+1)，那必然存在重复”；

也就是意味着我们只用使用一次O(n)的遍历时间，就可以确定一个范围的数字是否存在重复。这样的性质可以让我们不断地缩小所需要判断的数字范围，这也就是时间开销上的优化。

具体地，我们可以联想到二分法：

• 一开始将范围1~n分为两部分，一半是1~m，另一半是m+1~n；
• 如果范围1~m的数字的统计次数大于m，则这个范围内有重复的数字；否则另一半m+1~n的区间里一定有包含重复的数字；
• 继续二分存在重复数字的范围，重复步骤；
• 直到确定到某个重复数字。

比如说题目给的例子{ 2, 3, 5, 4, 3, 2, 6, 7 }：

• [1-4]范围的数字出现5次，[5-7]范围的数字出现3次，重复在[1-4];
• [1-2]范围的数字出现2次，[3-4]范围的数字出现3次，重复在[3-4]；
• [3]数字出现2次，[4]数字出现1次，重复数字是3。

然后简单分析一下时间复杂度，每次遍历统计的时间开销不变O(n)，因为数字范围二分，一共需要走O(logn)步，所以在O(nlogn)时间中可以找出重复数字。

完整代码实现：

#include <iostream>

bool is_repeat(int array[], int len, int start, int end) {
    int count = 0;
    for(int i = 0; i < len; i++) {
        if(array[i] <= end && array[i] >= start) {
            count += 1;
        }
    }
    return count > (end - start + 1);
}

int find_repeat(int array[], int len) {
    int start = 1;
    int end = len-1;
    while(end != start) {
        int mid = (end + start) / 2;
        if(is_repeat(array, len, start, mid)) {
            end = mid;
        } else {
            start = mid+1;
        }
    }
    return start;
}

int main() {
    int array[] = {2, 3, 5, 4, 3, 2, 6, 7};
    int len = sizeof(array) / sizeof(array[0]);
    int dup = find_repeat(array, len);
    printf("Repeat Number: %d\n", dup); // 3
    return 0;
}

Tips：上述代码没有考虑一些安全、边界问题，所以比较简短。

需要指出的一点是，上面的使用的这种方法不能保证找出所有重复的数字，例如其中的2也是重复数字，但是算法只找出了3，一个原因是因为只会检查其中一半范围，例如检查到前一半有重复的时候，就不会再检查后一半范围了，另一个原因是算法无法确定是其中一个数字出现2次还是几次。

---

面试题4：二维数组中的查找

在一个二维整数数组中，每一行从左到右递增，每一列从上到下递增，判断数组中是否含有指定数字。

例如：

$$ \begin{matrix} 1 & 2 & 8 & 9 \\ 2 & 4 & 9 & 12 \\ 4 & 7 & 10 & 13 \\ 6 & 8 & 11 & 15 \end{matrix} $$

当一个数和矩阵中间的一个数比较时，除了相等，还有两种情况：

• (a)当查询数字小于目标数字时，说明目标数字一定不会出现在左上角，剩下需要判断的区域在其右边和下边；
• (b)当查询数字大于目标数字时，说明目标数字一定不会出现在右下角，剩下需要判断的区域在其左边和上边。

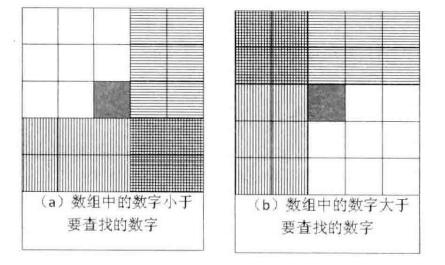
当我们按照常规思路，尝试从(0,0)出发，向右下角进行搜索时，我们跳转到下一格只有通过2种方式，从上转移到下，和从左转移到右，如果我们把已遍历的位置称为“已知信息”，我们可以看到这种搜索方式，大部分“已知信息”都集中在左上部，这在比较出现的两种情况中，要么无法提供任何信息，要么只能提供重叠区域的信息，无法让转移确定下一次的方向。

所以为了避免“已知信息”的浪费，我们可以尝试从右上角(0, n-1)出发，向左下角进行搜索，这样会提供更多的信息，如果发生向下转移，代表上边没有比目标数更大的，如果发生向左转移，代表右边的数比目标数更大，所以导致更加明确的在左下角区域中搜索目标数。

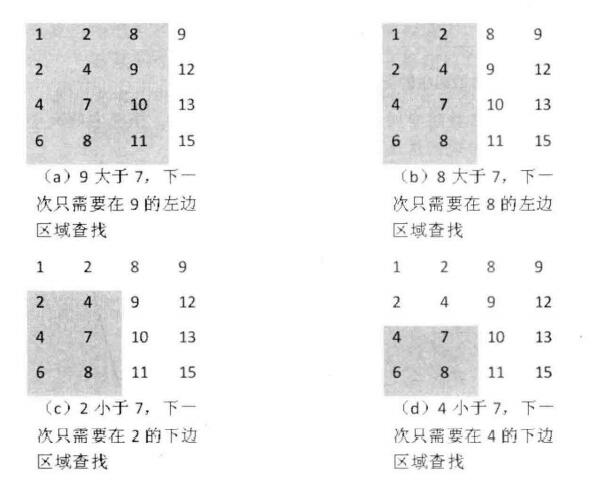
完整代码实现：

#include <iostream>

bool find(int matrix[][4], int rows, int cols, int target) {
    int i = 0;
    int j = cols - 1;
    while(i < rows && j >= 0) {
        if(matrix[i][j] < target) {
            i++;
        } else if(matrix[i][j] > target) {
            j--;
        } else {
            return true;
        }
    }
    return false;
}

int main() {
    int matrix[][4] = {
        {1, 2, 8, 9},
        {2, 4, 9, 12},
        {4, 7, 10, 13},
        {6, 8, 11, 15}
    };
    int target = 7;
    if(find(matrix, 4, 4, target)) {
        printf("Found!\n");
    } else {
        printf("Not Found!\n");
    }
    return 0;
}