《剑指Offer》第2章笔记 树

树的操作会涉及大量指针，因此与树相关的面试题都不太容易。

树的逻辑很简单：

• 除根节点之外，每个节点只有一个父节点，根节点没有父节点；
• 除叶节点之外，每个节点都有一个或多个子节点，叶节点没有子节点；
• 父节点和子节点之间用指针链接。

面试中大部分都是二叉树，在二叉树中每个节点最多只能有两个子节点。

二叉树中最重要的操作是如何遍历数结构，按照某种顺序访问树的所有节点，通常有几种遍历方式：

• 前序：父->左子->右子；
• 中序：左子->父->右子；
• 后序：左子->右子->父；
• 层序：从根节点层到叶节点层，按层输出，每一层按照从左到右输出。

二叉树中又有一些特例：

• 二叉搜索树：在二叉搜索树中，左子节点总是小于或等于父节点，右子节点总是大于或等于父节点，可以平均在O(logn)的时间内根据值在二叉树中查找节点；
• 堆：堆分为最大堆和最小堆，在最大堆中，根节点的值最大，最小堆中的根节点值最小（其他节点按子树递推），有很多需要快速找到最大值或最小值的问题都可以用堆来解决；
• 红黑树：把树中的节点定义为红、黑两种颜色，并通过规则确保从根节点到叶节点的最长路径的长度不超过最短路径的两倍；在C++的STL中，set、multiset、map、multimap等都是基于红黑树实现的。

面试题7：重建二叉树

输入二叉树的前序和中序遍历结果，重建该二叉树，假设输入的前序中序结构中都不含有重复的数字。

// 二叉树节点定义
struct Node {
  int value;
  Node* left;
  Node* right;
}

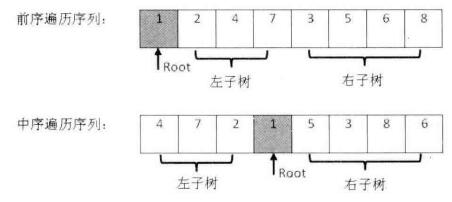
在前序遍历中，第一个数字总是树的根节点；但在中序遍历中，根节点的值在序列中间，左子树的值位于根节点左边，右子树的值位于根节点右边；所以对于一个子树，我们在前序中寻找其根节点（第一个出现的值），然后在中序中根据根节点的位置，把剩下的点分为左子树和右子树。

完整代码实现：

#include <iostream>
#include <exception>

struct Node {
    int value;
    Node* left;
    Node* right;
};

Node* construct_core
(
    int* po_start, int* po_end,
    int* io_start, int* io_end
) {
    int root_value = po_start[0];
    Node* root = new Node();
    root->value = root_value;
    root->left = root->right = nullptr;
    if(po_start == po_end) {
        if(io_start == io_end && *po_start == *io_start) {
            return root;
        } else {
            // Windows Ver Error
            std::logic_error ex("Invalid input");
            throw std::exception(ex);
        }
    }

    int* io_root = io_start;
    while(io_root <= io_end && *io_root != root_value) {
        io_root++;
    }

    if(io_root == io_end && *io_root != root_value) {
        // Windows Ver Error
        std::logic_error ex("Invalid input");
        throw std::exception(ex);
    }

    int left_len = io_root - io_start;
    int* left_po_end = po_start + left_len;

    if(left_len > 0) {
        root->left = construct_core(po_start+1, left_po_end, io_start, io_root-1);
    }
    if(left_len < po_end - po_start) {
        root->right = construct_core(left_po_end + 1, po_end, io_root+1, io_end);
    }

    return root;
}

Node* construct(int* preodr, int* inodr, int len) {
    if(preodr == nullptr || inodr == nullptr || len <= 0) {
        return nullptr;
    } else {
        return construct_core(preodr, preodr + len - 1,
            inodr, inodr + len - 1);
    }
}

void post_order_print(Node* node) {
    if(node != nullptr) {
        post_order_print(node->left);
        post_order_print(node->right);
        printf("%d ", node->value);
    }
}

int main() {
    int preodr[8] = {1, 2, 4, 7, 3, 5, 6, 8};
    int inodr[8] = {4, 7, 2, 1, 5, 3, 8, 6};
    Node* root = construct(preodr, inodr, 8);
    post_order_print(root); // 7 4 2 5 8 6 3 1
    return 0;
}

面试题8：二叉树的下一个节点

给定二叉树和其中的一个节点，如何找出中序遍历序列的下一个节点？树节点除了有左右子节点指针，还有一个指向父节点的指针。

这类题目一般从各类情况具体分析入手：

• 如果节点有右子树，则下一个节点就是右子树中的最左子节点；
• 如果节点没有右子树：
  • 如果该节点是父节点的左子节点，父节点就是下一个节点；
  • 并且该节点是父节点的右子节点，按照中序遍历的逻辑，需要继续往上寻找，直到找到某一个节点A，这个节点A是A父节点的左子节点，如果不存在这样的节点，那就代表原节点为最后一个遍历节点了，没有下一个节点。

面试中遇到这种题，大概率只需要编写指定功能的函数部分，不需要编写完整的代码，所以需要对面试官询问具体的输入输出情况。

#include <iostream>

struct Node {
    int value;
    Node* left;
    Node* right;
    Node* parent;
};

Node* find_next(Node* node) {
    if(node == nullptr) {
        return nullptr;
    }

    Node* next = nullptr;
    if(node->right != nullptr) {
        // 右子树的最左子节点（不一定需要是叶节点）
        Node* temp = node->right;
        while(temp->left != nullptr) {
            temp = temp->left;
        }
        next = temp;
    } else if (node->parent != nullptr) {
        // 寻找满足条件的祖先节点
        // 某个节点是其父节点的左子节点
        Node* temp = node;
        Node* parent = node->parent;
        while(parent != nullptr && temp == parent->right) {
            temp = parent;
            parent = parent->parent;
        }
        next = parent;
    }

    return next;
}