《实时渲染 4th》第1章笔记 导论
实时渲染一般指计算机里的快速图像生成。
PS:原书《Real Time Rendering 4th》全英文,有些词翻译如果不够好还请见谅。
Tips:屏幕刷新率(refresh rate)和显示频率(display rate)在现在是有区别的;
We will not be able to cover every topic in depth, so our goal is to present key concepts and terminology, explain the most robust and practical algorithms in the field, and provide pointers to the best places to go for more information.
虽然这本书没有覆盖到实时渲染涉及到的每一个主题,但本书的目的是呈现关键概念和术语、解释最鲁邦和实用的算法、提供深入了解这些内容的方向指引。
1 内容概览
- 第2章 图形渲染管线:
The Graphics Rendering Pipeline,实时渲染的核心是通过什么样的步骤来将场景传达到显示上; - 第3章 图形处理单元:
The Graphics Processing Unit,现代GPU中一般通过一组计算单元(fixed-function and programmable units)来实现渲染管线; - 第4章 变换:
Transforms,变换是操作物体位置、方向、大小以及形状、控制摄像机位置和视角的基本工具; - 第5章 着色基础:
Shading Basics,着色一般指的是通过材质(Material)和光源(Light)来表现物体,还有一些相关的主题,例如抗锯齿(反走样 antialiasing)、透明处理以及Gamma矫正; - 第6章 纹理:
Texturing,纹理贴图用于在物体表面呈现纹理; - 第7章 光影:
Shadows,光影让场景更有真实情感,会介绍一些快速计算光影的流行算法; - 第8章 光和颜色:
Light and Color,讲解计算机是如何如何量化光和颜色,以及把这些量化转换成显示量纲的方法; - 第9章 基于物理的着色:
Physically Based Shading,基于物理的着色会更加接近真实; - 第10章 局部光照:
Local Illumination,主要介绍一些渲染复杂光源的算法,例如光源本身具有物理形状; - 第11章 全局光照:
Global Illumination,模拟光源和场景之间的交互的算法,进一步增加场景的真实度; - 第12章 图像效果:
Image-Space Effects,GPU擅长快速处理图像,首先介绍图像滤波(image filtering)和重投影(reprojection)技术,然后介绍一些流行的后期效果,例如镜头光晕(lens flares)、动态模糊(motion blur)以及景深(depth of field); - 第13章 几何之外:
Beyond Polygons,三角形不一定总是最快或最真实地描述物体的方式,还有其他方式,例如图片(images)、点云(point clouds)、体素(voxels)等; - 第14章 体渲染和透光渲染:
Volumetric and Translucency Rendering,介绍体积材质(volumetric material)(例如云、烟、雾)的表达方式以及和光的交互,大到气象效果,小到头发渲染; - 第15章 非真实渲染:
Non-Photorealistic Rendering,主要介绍一些风格渲染,例如卡通渲染(cartoon shading)、水彩效果(watercolor
effects); - 第16章 几何技术:
Polygonal Techniques,几何体数据的来源各种各样,如果需要又快又好地渲染,就需要进行一定处理,涉及到几何数据表达和压缩方法; - 第17章 曲线和曲面:
Curves and Curved Surfaces,复杂的表面表达提供的优势在于更好的在质量和速度中进行取舍,表达越简洁,曲面就越光滑; - 第18章 管线优化:
Pipeline Optimization,寻找渲染瓶颈来优化速度,涉及到一些多线程技术; - 第19章 加速算法:
Acceleration Algorithms,比快更快,Various
forms of culling and level of detail rendering are covered; - 第20章 高效着色:
Efficient Shading,越多的光源,渲染就越慢,在渲染前无法知道是否需要渲染会造成资源浪费,使用一些方法可以解决这些问题; - 第21章 虚拟现实和增强现实:
Virtual and Augmented Reality,这些领域有很多特定的技术难题,也有一些相应方法来高效快速的生成图像; - 第22章 相交检测:
Intersection Test Methods,深入介绍一些几何相交检测的高效算法; - 第23章 图形硬件:
Graphics Hardware,图形硬件的一些细节,例如色彩深度(color depth)、帧缓冲(framebuffers)和基础架构类型; - 第24章 面向未来:
The Future,Take a guess (we do)。
还有一些没有收录在实体书中,在realtimerendering.com上更新的章节:
- 碰撞检测:
Collision Detection,The 3rd edition’s chapter on this subject has been fully updated, but could not fit in the bounds of the physical book; - 实时光线追踪:
Real-Time Ray Tracing,API support for this area was announced in March 2018, too late for inclusion in the book, so we wrote an additional chapter about the subject as a whole. - 附录:
Appendices,The two appendices, Some Linear Algebra and Trigonometry, also had to be cut from the physical book.
2 标记和定义
2.1 数学标记
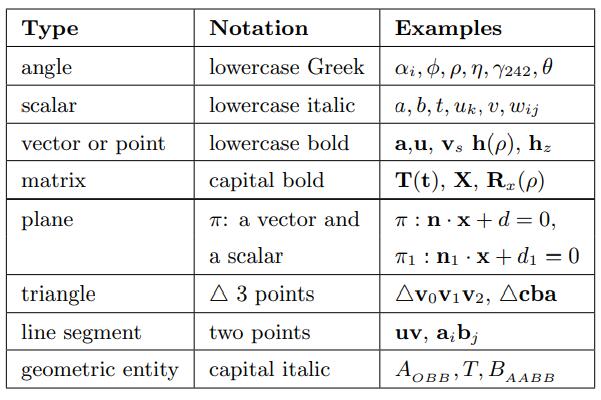
向量或者点通常用粗体小写字母表示,并且其内部组成一般写为:
在图形学领域中一般用列向量的表达方式,有时候为了书面方便也会写成行向量。
书中使用到矩阵大多是 \(2 \times 2\),\(3 \times 3\) 和\(4 \times 4\),以\(3 \times 3\)矩阵为例,说明矩阵的表示方式:
有时候为了表达需求,会只关注行向量或者列向量的内容,矩阵也可以写为:
其中 \(\textbf{m}_{,j}\) 代表第j列向量,\(\textbf{m}_{i,}\) 代表第i行向量。
平面的数学表示是 \(\pi:\textbf{n}\cdot\textbf{x} + d = 0\),其中 \(\textbf{n}\)是平面的法向量,\(d\)是标量,平面将空间分为两个子空间,正子空间是 \(\textbf{n}\cdot\textbf{x} + d > 0\),相应的负子空间是 \(\textbf{n}\cdot\textbf{x} + d < 0\)
三角形通常用三个点来表示,例如有不共线的三点 \(\textbf{v}_{0}, \textbf{v}_{1}, \textbf{v}_{2}\),构成的三角形是 \(\bigtriangleup\textbf{v}_{0}\textbf{v}_{1}\textbf{v}_{2}\)。
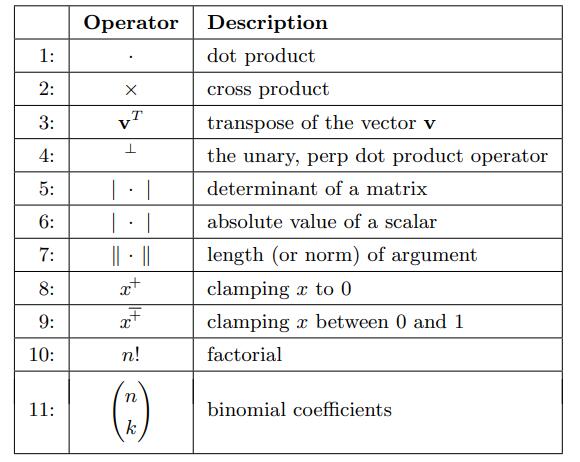
大部分都应该是比较常见的,需要稍微特殊说明的几个:
- 主要用于二维向量,求二维向量的垂直向量,例如有 \(\textbf{v}=(v_{x}, v_{y})\),\(\textbf{v}^{\perp}=(-v_{y}, v_{x})\);
- 将x映射为非负空间数,当其为负值时会变为0;
- 和8较为类似,映射到0-1空间中,大于1变为1,小于0变为0;
binomial coefficients,二项式系数,\(\left(\begin{matrix}n \\ k\end{matrix}\right) = \frac{n!}{k!(n-k)!}\)。
一般把 \(x=0, y=0, z=0\) 叫做 坐标平面(coordinate
planes)或者轴对齐平面(axis-aligned planes),将轴 \(\textbf{e}_{x}=(1, 0, 0), \textbf{e}_{y}=(0, 1, 0), \textbf{e}_{z}=(0, 0, 1)\)叫做主轴(main axes)或者主方向(main directions),也分别叫做x轴(x-axis),y轴(y-axis)和z轴(z-axis)。
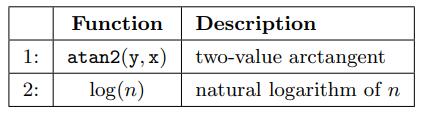
C语言数学函数 atan2(y,x) 有时候被经常提及到,它是arctan(x)的一个拓展,主要区别在于 \(-\frac{\pi}{2} < arctan(x) < \frac{\pi}{2}\),\(0 \lep atan2(y, x) < 2\pi\),一种常用操作是计算arctan(y/x),但是当x=0时会出现除0问题(尽管可能本意是表达一个无穷大数,但C语言会报除0错误),而这时候使用atan2(y,x)可以避免这样的问题。
log(n)函数一般指的是自然数e为底数,而不是以10为底数。
默认情况下均使用右手坐标系。
颜色一般用一个三元向量表示,(red, green, blue),各项的值都在[0,1]。
2.2 几何定义
最原石的一些基础渲染元(basic rendering primitives, also called drawing primitives),最常用的是点、线和三角形。
在本书中,一组几何体(a collection of geometric entities)通常叫做一个模型(model)或者对象(object);场景(scene)指的是环境中一组需要渲染模型,场景一般也包括材质描述、光线以及视角定义。
也有些不是使用点、线和三角形这种基础渲染元表达的模型,例如点云、函数表达(贝塞尔曲线)。
2.3 Shading和Shader?
本书中的 Shading 和 Shader 是两个截然不同但是又有关联的概念:
- 前者指的是计算机生成的视觉表达(computer-generated visual appearance),例如shading model、shading equation以及toon shading这些概念原理;
- 后者指的是渲染系统中的一个可编程单元,例如vertex shader、shading language。
尽管他们用词形式上有一些混淆,但是要通过语境上下文来判断其指的是哪个概念(在书本以外可能会单独开一页来讲一些概念的区分)。
《实时渲染 4th》第1章笔记 导论


