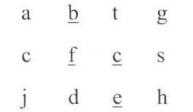考算法的面试题也备受面试官青睐(老折磨人了)。
通常排序和查找 是面试时考查算法的重点,准备的时候要重点掌握二分查找、归并排序和快速排序,要做到随时正确、完整地写出它们地代码。
二维数组上搜索路径的一些题目可以尝试用回溯法,通常回溯法适合用递归代码实现,如果面试官不允许递归实现,再尝试用栈来模拟递归过程。
如果是求解某个问题的最优解,并且问题可以分为子问题解决,就可以尝试用动态规划,如果在分解子问题中,满足一些特定条件就可以找到最优解,可以考虑用贪婪最优法。
1 递归和循环 递归的代码通常比循环更加简洁,但代价是效率不够高,并且还有递归栈层数限制; 在一些题目中简单的递归会增加不必要的重复计算; 应用动态规划解决问题时,大部分都是递归方法分析问题,有些问题会出现子问题重复计算,到时候会讨论如何用循环替换递归实现; 面试题10:斐波那契数列
题目一:求斐波那契数列的第n项,f(0) = 0, f(1) = 1, f(n) = f(n-1) + f(n-2)。
最简单的递归法就不在说明了,这里直接写一下不用重复计算的思路,当需要求解第n项时,需要求解前n-1项,通过观察可以发现从第2项开始计算,可以避免重复计算的问题。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 #include <iostream> #include <algorithm> const int max_n = 1000 ;long long store[max_n];long long fibonacci (unsigned n) if (n >= max_n) { return -1 ; } else if (store[n] != -1 ) { return store[n]; } else { for (int i = 2 ; i <= n; i++) { store[i] = store[i-1 ] + store[i-2 ]; } return store[n]; } } int main () std ::fill(&store[0 ], &store[max_n], -1 ); store[0 ] = 0 ; store[1 ] = 1 ; std ::cout << fibonacci(50 ) << std ::endl ; return 0 ; }
书上还有一个O(logn)的算法,要使用到一个数学公式:
$$ \left[ \begin{matrix} f(n) & f(n-1) \\ f(n-1) & f(n-2) \end{matrix} \right] = \left[ \begin{matrix} 1 & 1 \\ 1 & 0 \end{matrix} \right]^{n-1} $$
公式可以用数学归纳法证明,问题就转换为如何求矩阵乘方,如果只是简单地从0开始循环,n次方需要n次元素,时间复杂度仍然是O(n),并不比前面的方法快,但是其中的乘方有如下性质:
$$ a^{n} = \left\{ \begin{array}{rcl} a^{n/2} \cdot a^{n/2}, & & n\ is\ even \\ a^{(n-1)/2} \cdot a^{(n-1)/2} \cdot a, & & n\ is\ odd \end{array} \right. $$
从公式可以看出,如果想求得n次方,就要先求得n/2次方,再把n/2次方的结果平方一下即可,时间复杂度为O(logn)。
不过算法仅做了解,很少会这么去写,实现起来也比较复杂。
还有不少面试题可以看成是斐波那契数列的应用:
题目二:青蛙跳台阶问题。
一只青蛙一次可以跳上1级台阶,也可以跳上2级台阶,求该青蛙跳上一个n级的台阶总共有多少种跳法。
将问题看作是求解函数f(n),当青蛙第1次跳1级,则下一次求解f(n-1),如果青蛙第1次跳2级,则下一次求解f(n-2),所以其实本质还是斐波那契数列f(n)=f(n-1)+f(n-2)。
2 查询和排序 查询相对于排序较为简单,不外乎顺序查找、二分查找、哈希表查找和二叉排序树查找。完整正确地二分查找代码 ,否则可能连继续面试的兴趣都没有。
排序比查找要复杂一点,面试官会经常要求应聘者比较 插入排序、冒泡排序、归并排序、快速排序等不同算法的优劣。
实现快速排序算法的关键在于先在数组中选择一个数字,接下来把数组中的数字分为两部分,比选择的数字小的数字移到数组左边,比选择的数字大的数字移到数组的右边(递增排序)。
(然后就是一段基本上在哪本书上都能看到的快速排序代码)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 int partition (int data[], int len, int start, int end) if (data == nullptr || len <=0 || start < 0 || end >= len) { std ::logic_error ex ("Invalid Parameters" ) throw std ::exception(ex); } int index = random_in_range(start, end); swap(&data[index], &data[end]); int small = start - 1 ; for (index = start; index < end; index++) { if (data[index] < data[end]) { small++; if (small != index) { swap(&data[index], &data[small]); } } } small++; swap(&data[small], &data[end]); return small; }
上面是partition部分的代码,快速排序的其中一步,选择锚元素(比较元素),将数组start-end区域的元素划分为两部分,一部分小于锚元素,另一部分大于锚元素。
完整的运行代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 #include <iostream> #include <cstdlib> #include <ctime> #include <exception> int random_in_range (int start, int end) srand((unsigned )time(NULL )); return rand() % (end - start + 1 ) + start; } void swap (int * lhs, int * rhs) int temp = *lhs; *lhs = *rhs; *rhs = temp; } int partition (int data[], int len, int start, int end) if (data == nullptr || len <=0 || start < 0 || end >= len) { std ::logic_error ex ("Invalid Parameters" ) throw std ::exception(ex); } int index = random_in_range(start, end); swap(&data[index], &data[end]); int small = start - 1 ; for (index = start; index < end; index++) { if (data[index] < data[end]) { small++; if (small != index) { swap(&data[index], &data[small]); } } } small++; swap(&data[small], &data[end]); return small; } void quick_sort (int data[], int len, int start, int end) if (start == end) { return ; } int index = partition(data, len, start, end); if (index > start) { quick_sort(data, len, start, index-1 ); } if (index < end) { quick_sort(data, len, start+1 , end); } } int main () int data[] = {9 , 1 , 2 , 7 , 5 , 2 , 3 , 5 , 4 , 6 }; quick_sort(data, 10 , 0 , 9 ); for (int i = 0 ; i < 10 ; i++) { printf ("%d " , data[i]); } return 0 ; }
partition函数除了可以用在快速排序中,还可以用来实现在长度n数组中查找第k大的数字,面试题39“数组中出现次数超过一半的数字”和面试题40“最小的k个数”都可以用这个函数来解决。
不同排序的适用场合也不尽相同,快速排序虽然总体的平均效率最好,但不是任何时候都是最优的算法(只是在平均效率上满足O(nlogn),可以找出一些最坏的情况),所以在面试的时候,如果面试官要求实现一个排序算法,可以先问清楚这个排序应用的环境是什么 、有哪些约束条件 等等,得到足够多的信息之后再选择合适的排序算法。
面试题11:旋转数组的最小数字
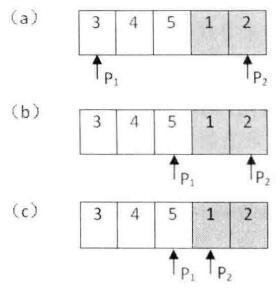
把一个数组最开始的若干的元素搬到数组的末尾,称之为数组的旋转,输入一个递增排序的数组的一个旋转,输出旋转数组的最小元素。例如{3, 4, 5, 1, 2}是{1, 2, 3, 4, 5}的一个旋转,数组的最小值是1。
思路1:简单遍历数组求最小值(无论正序还是逆序),时间开销都是O(n),大概率不是一个最优解; 思路2:递增排序的一个区间满足性质, 首元素一定小于尾元素 ,如果考虑到元素可以重复,即如果首元素大于等于尾元素 ,则该区间可能并不是非递减的 。 思路3:思路2通过二分区间判断实现起来还是有一点复杂,还可以进一步地简化思路,每一次判断mid和start、end位置上元素大小关系,如果mid>=start,证明mid位于前面的递增区间,下一步在mid-end中找最小元素;如果mid<=end,证明mid位于后面的递增区间,下一步在start-mid中找最小元素。 按照思路3,start总是指向前面递增数组的元素、end总是指向后面递增数组的元素,当start和end中间没有其他元素时,end就指向后面递增元素的第一个,也就是最小的数字,这也是循环结束的条件。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 int min (int * numbers, int len) if (numbers == nullptr || len <= 0 ) { std ::logic_error ex ("Invalid parameters" ) throw std ::exception(ex); } int index1 = 0 ; int index2 = len - 1 ; int index_mid = index1; while (numbers[index1] >= numbers[index2]) { if (index2 - index1 == 1 ) { index_mid = index2; break ; } index_mid = (index1 + index2) / 2 ; if (numbers[index_mid] >= numbers[index1]) { index1 = index_mid; } else if (numbers[index_mid] <= numbers[index2]) { index2 = index_mid; } } return numbers[index_mid]; }
但上面的方法还有一些特殊情况没有考虑到:
如果只搬动了0个元素到后面,即排序数组本身,上面的方法就不再适用了,但因为此时数组中一个数字就是最小的数字,可以直接返回; 如果index1和index2指向的元素相等,甚至他们都和index_mid指向的元素想等时,应该如何处理呢?这个时候无法简单地判断出min在前面还是后面(参考下面图),所以只能采取简单的遍历法(如果是递归函数实现的话可以都向下计算然后比对最小值)。 完整代码实现:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 #include <iostream> #include <exception> int min_in_order (int * numbers, int start, int end) int min = numbers[start]; for (int i = start + 1 ; i <= end; i++) { if (min > numbers[i]) { min = numbers[i]; } } return min; } int min (int * numbers, int len) if (numbers == nullptr || len <= 0 ) { std ::logic_error ex ("Invalid parameters" ) throw std ::exception(ex); } int index1 = 0 ; int index2 = len - 1 ; int index_mid = index1; while (numbers[index1] >= numbers[index2]) { if (index2 - index1 == 1 ) { index_mid = index2; break ; } index_mid = (index1 + index2) / 2 ; if (numbers[index1] == numbers[index2] && numbers[index_mid] == numbers[index1]) { return min_in_order(numbers, index1, index2); } else if (numbers[index_mid] >= numbers[index1]) { index1 = index_mid; } else if (numbers[index_mid] <= numbers[index2]) { index2 = index_mid; } } return numbers[index_mid]; } int main () int numbers[] = {3 , 4 , 5 , 1 , 2 }; printf ("%d\n" , min(numbers, 5 )); int onumbers[] = {1 , 1 , 1 , 0 , 1 }; printf ("%d\n" , min(onumbers, 5 )); return 0 ; }
3 回溯法 回溯法可以看成蛮力法的升级,它从解决问题的每一步可能选项理选出一个可行的解决方法。
用回溯法解决的问题的所有选项可以形象地用树状结构表示。在某一步有n个可能的选项,该步骤可以看成是树状结构中的一个节点,每个选项看成树中节点连接线。树的叶节点对应对应着终结状态,如果在叶节点的状态满足题目的约束条件,则找到了一个可行的解决方案。
如果叶节点的状态不满足约束,则只好回溯到它的上一个节点再尝试其他的选项,如果上一个节点所有可能的选项都已经试过,找下一种可能选项时,需要再次回溯到上一个节点(依次类推)。如果所有节点的所有选项都已经尝试过仍然不能达到满足约束条件的终结状态,则该问题无解。
以面试题12来说明回溯法的应用方法。
面试题12:矩阵中的路径
设计一个函数,用来判断一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一格开始,每一步可以在矩阵中向左、右、上、下移动一格。如果一条路径经过了矩阵的某一格,那么该路径不能再次进入该格子。
用回溯法解决的典型题,首先在矩阵中任选一个格子作为路径的起点,然后尝试匹配字符串,如果位置字符匹配,则在临近格子中寻找下一步格子,重复上述过程,直到路径上所有字符都在矩阵中找到相应的位置。
由于回溯法的递归特性,路径可以被看成一个栈,当在矩阵中定位了路径中前n个字符位置之后,在与第n个字符对应的格子的周围都没有找到第n+1字符,这时候只好在路径上回到第n-1字符,重新定位第n个字符。
由于路径不能重复进入矩阵的格子,所以要定义和字符矩阵大小一样的布尔值矩阵,用来标识路径已经进入了哪些格子。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 #include <iostream> #include <cstring> // include memset() bool has_path_core (const char * matrix, int rows, int cols, int row, int col, const char * str, int & path_len, bool * visited) if (str[path_len] == '\0' ) { return true ; } bool has_path = false ; if (row >= 0 && row < rows && col >= 0 && col < cols && matrix[row * cols + col] == str[path_len] && !visited[row * cols + col]) { path_len++; visited[row*col + col] = true ; has_path = has_path_core(matrix, rows, cols, row, col-1 , str, path_len, visited) || has_path_core(matrix, rows, cols, row-1 , col, str, path_len, visited) || has_path_core(matrix, rows, cols, row, col+1 , str, path_len, visited) || has_path_core(matrix, rows, cols, row+1 , col, str, path_len, visited); if (!has_path) { path_len--; visited[row * cols + col] = false ; } } return has_path; } bool has_path (char * matrix, int rows, int cols, char * str) if (matrix == nullptr || rows < 1 || cols < 1 || str == nullptr ) { return false ; } bool * visited = new bool [rows * cols]; memset (visited, 0 , rows * cols); int path_len = 0 ; for (int row = 0 ; row < rows; row++) { for (int col = 0 ; col < cols; col++) { if (has_path_core(matrix, rows, cols, row, col, str, path_len, visited)) { return true ; } } } delete [] visited; return false ; } int main () char matrix[12 ] = { 'a' ,'b' ,'t' ,'g' , 'c' ,'f' ,'c' ,'s' , 'j' ,'d' ,'e' ,'h' }; char str1[10 ] = "bfce" ; if (has_path(matrix, 3 , 4 , str1)) { std ::cout << str1 << " in matrxi." << std ::endl ; } else { std ::cout << str1 << " not in matrxi." << std ::endl ; } char str2[10 ] = "abfb" ; if (has_path(matrix, 3 , 4 , str2)) { std ::cout << str2 << " in matrxi." << std ::endl ; } else { std ::cout << str2 << " not in matrxi." << std ::endl ; } return 0 ; }
面试题13:机器人的运动范围
地上有一个m行n列的方格。一个机器人从(0,0)的格子开始移动,它每次可以向左、右、上、下移动一格,但不能进入行坐标和列坐标的数位之和 大于k的格子。例如,当k为18时,机器人能进入方法(35, 37),因为3+5+3+7=18,但不能进入方格(35, 38),因为3+5+3+8=19,请问该机器人能够到达多少格子?
机器人从(0,0)开始移动,准备进入(i,j)时,要检查坐标的数位来判断是否能够进入,如果能进入,再判断是否能进入4个相邻的格子(不包含已走格子)。
完整代码实现:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 #include <iostream> int get_digit_sum (int num) int sum = 0 ; while (num > 0 ) { sum += num % 10 ; num /= 10 ; } return sum; } bool check (int threshold, int rows, int cols, int row, int col, bool * visited) if (row >= 0 && row < rows && col >= 0 && col < cols && get_digit_sum(row) + get_digit_sum(col) <= threshold && !visited[row * cols + col]) { return true ; } return false ; } int moving_count_core (int threshold, int rows, int cols, int row, int col, bool * visited) int count = 0 ; if (check(threshold, rows, cols, row, col, visited)) { visited[row * cols + col] = true ; count = 1 + moving_count_core(threshold, rows, cols, row - 1 , col, visited) + moving_count_core(threshold, rows, cols, row, col - 1 , visited) + moving_count_core(threshold, rows, cols, row + 1 , col, visited) + moving_count_core(threshold, rows, cols, row, col + 1 , visited); } return count; } int moving_count (int threshold, int rows, int cols) if (threshold < 0 || rows <= 0 || cols <= 0 ) { return 0 ; } bool *visited = new bool [rows * cols]; for (int i = 0 ; i < rows * cols; i++) { visited[i] = false ; } int count = moving_count_core(threshold, rows, cols, 0 , 0 , visited); delete [] visited; return count; } int main () std ::cout << moving_count(-1 , 1 , 1 ) << std ::endl ; std ::cout << moving_count(0 , 1 , 1 ) << std ::endl ; std ::cout << moving_count(12 , 40 , 40 ) << std ::endl ; std ::cout << moving_count(18 , 40 , 40 ) << std ::endl ; return 0 ; }
4 动态规划与贪婪算法 如果面试题是求一个问题的最优解(通常是求最大值或者最小值 ),而且该问题能够被分解成若干个子问题,子问题之间还有重叠的更小子问题,就可以考虑用动态规划来解决这个问题。
在应用动态规划之前,要先分析是否能把大问题分解成小问题 ,分解后的每个小问题也存在最优解 ,如果把小问题的最优解组合起来能够得到整个问题的最优解 ,则可以应用动态规划来解决这个问题。
在一些题目情况中,相同子问题在分解大问题的过程中重复出现,为了避免重复求解相同子问题,可以用从下往上的顺序先计算小问题的最优解并存储下来,再以此为基础求取大问题的最优解。在应用动态规划解决问题的时候,我们总是从解决最小问题开始,并把已经解决的子问题的最优解存储下来(大部分题目一般用一维或者二维数组里),并把子问题的最优解组合起来逐步解决大的问题。
在应用动态规划时,每一步都面临若干个选择,在求解时只能把所有的可能尝试一遍,然后比较得出最优的选择。
贪婪算法和动态规划不一样,贪婪算法每一步都可以根据规则做出一个最优的选择,基于这个找到最优解,但贪婪算法需要证明每一步的选择是可以保证最后获得最优结果,有时候不要想当然的应用贪婪算法。
面试题14:剪绳子
给你一根长度为n的绳子,请把绳子剪成m段(m、n都是整数,n>1并且m>1),每段绳子的长度记为k[0],k[1],...,k[m],请问 k[0] x k[1] x ... x k[m]可能的最大乘积是多少?例如,当绳子的长度是8时,我们把它剪成长度分为2、3、3的三段,此时得到的最大乘积是18。
Tips:这道题里面的一个比较含糊不清的地方是对m的界定,有些题目中可能m也是一个输入量,指计算在这个m段限定条件下n长度绳子的最大结果值(基本上就是另一类题了),而在本书的这道题目中并没有将m看作一个单独的输入量,只是说明后续的计算流程用,在面试遇到这样的情况可以向面试官询问对m的作用界定。
思路1:暴力遍历,第一步有n-1种剪法,第二步有n-2种剪法,…,剪到底的话需要剪n步(每一步可以剪多个绳子),所以可以简单估算时间复杂度O(n^2); 思路2:动态规划; 思路3:尝试用贪婪算法来解决。 先讲一下动态规划的解法 。
首先定义函数f(n)为把长度为n的绳子剪成若干段后各段长度乘积的最大值。在剪第一刀时,有n-1中可能的选择,因此有f(n)=max(f(i) x f(n-i)),其中0<i<n。
这是一个从上至下的递归公式,递归会产生很多重复计算,所以一个更好的办法是按照从下而上的顺序计算,也就是说我们先得到f(2)、f(3),再得到f(4)、f(5),直到得到f(n)。比较容易得知f(1)=0、f(2)=1以及f(3)=2,之后就按照迭代公式计算,得到f(n)。
Tips:书上这个题目的解析里面,个人觉得有一点疏漏,f(k-1)的定义应该是在剪后的乘积最大 和不剪的自身长度 中的最大值,即f(k-1)=max({f(i) x f(k-i), k=1,2,...,n-1}),,因为只有在计算f(n)的时候是必须要剪断的(因为m>1),而剩下的子段不是一定要剪断,所以f(k-1), k=1,2,...,n-1的计算方式不能完全照搬f(n)的公式,例如f(1)作为一个长度为1的子段,因为并不是一定要剪,所以其本身可以返回的最大长度是1,而不是0,否则对于一个长度为n的绳子,在剪为1长度和n-1长度的两个子段时,使用f(1)=0,就会导致计算的结果错误,因为在这个情况下是有最后的值的,而并不是0*f(n-1)=0,所以按照修正后的定义,当是子段的时候,f(1)=1,f(2)=2,f(3)=3,f(4)=4,f(5)=6,…,可以发现虽然在k>3这部分定义修正没有意义,但对于k<=3部分是有意义的。
完整实现代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 #include <iostream> int max_product_after_cutting_dyprog (int len) if (len < 2 ) { return 0 ; } if (len == 2 ) { return 1 ; } if (len == 3 ) { return 2 ; } int * products = new int [len + 1 ]; products[0 ] = 0 ; products[1 ] = 1 ; products[2 ] = 2 ; products[3 ] = 3 ; int max = 0 ; for (int i = 4 ; i <= len; i++) { max = 0 ; for (int j = 1 ; j <= i/2 ; j++) { int product = products[j] * products[i - j]; if (max < product) { max = product; } } products[i] = max; } max = products[len]; delete [] products; return max; } int main () std ::cout << max_product_after_cutting_dyprog(10 ) << std ::endl ; return 0 ; }
Tips:上面的代码除了调整过一行的位置以外,基本上没有修改,可以看到代码中对f(1)、f(2)和f(3)的定义都是符合我之前说的修正后的定义,而不是作者说明的什么f(1)=0、f(2)=1以及f(3)=2,所以也侧面证明之前我对定义的修正是正确的。
接着看一下贪婪算法的解法 。
如果按照如下的策略来剪绳子,则得到的各段绳子的长度乘积最大,当n>=5时,尽可能多地剪长度为3的绳子;当剩下的绳子长度为4时,把绳子剪成两段长度为2的绳子。
完整实现代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 #include <iostream> #include <cmath> int max_product_after_cutting_greedy (int len) if (len < 2 ) { return 0 ; } if (len == 2 ) { return 1 ; } if (len == 3 ) { return 2 ; } int times_of_3 = len / 3 ; if (len - times_of_3 * 3 == 1 ) { times_of_3 -= 1 ; } int times_of_2 = (len - times_of_3 * 3 ) / 2 ; return (int )(pow (3 , times_of_3) * pow (2 , times_of_2)); } int main () std ::cout << max_product_after_cutting_greedy(10 ) << std ::endl ; return 0 ; }
证明一些这种思路的正确性:
首先,当n>=5时,我们可以证明2(n-2)>n并且3(n-3)>n(剪出一长度2子段或剪出一长度3子段),也就是说,当绳子剩下的长度大于等于5时,就把它剪成3或者2的子段,另外,n>=5时,3(n-3)>=2(n-2),因此我们应该尽可能地多剪长度为3的绳子段(其实书上的这部分证明还并不够严谨,可以自行去严谨地证明 )。 那么当长度为4时,可以简单推出最大的情况就是2*2或者不剪的4。 5 位运算 位运算是把数字用二进制表示 之后,对每一位上0或者1的运算,二进制及其位运算是现代计算机学科的基石,很多底层的技术都离不开位运算(都是基石了咋离得开嘛),因为与位运算相关的题目也经常出现在面试中。
在微软产品Excel中,用A表示第1列,B表示第2列,…,Z表示第26列,AA表示第27列,AB表示第28列,…,以此类推,写出一个函数,输入用字母表示的列号,输出第几列,这就是一个典型的进制转换题目。
位运算总共只有5种运算:与 &、或 ||、异或 ^、左移<<和右移>>。
与、或和异或运算规律可以用下表进行总结:
左移运算法m << n表示把m左移n位,在左移n位时,最左边的n位将被丢弃,同时在最右边补上n个0,比如:
1 2 00001010 << 2 = 00101000 10001010 << 3 = 01010000
右移运算符m >> n表示把m右移n位,在右移n位时,最右边的n位将被丢弃,但是在右移时处理最左边位的情形要稍微复杂一点:
如果数字是一个无符号数值,则用0填补最左边的n位; 如果数字是一个有符号数值,则用数字的符号位填补最左边的n位; 1 2 00001010 >> 2 = 00000010 10001010 >> 3 = 11110001
面试题15“二进制中1的个数”就是直接考查位运算的例子,而面试56“数组中数字出现的次数”、面试题65“不用加减乘除做加法”等都是根据位运算的特点来解决问题。
面试题15:二进制中1的个数
实现一个函数,输入一个整数,输出该数二进制表示中1的个数,例如,把9表示成二进制是1001,有2个1,所以输出2。
可能会引起死循环 的解法:判断整数二进制最右边是否为1,然后进行右移一位再进行判断,直到整个整数变为0为止,至于如何判断一个整数的最右边是不是1,只要把整数和1做位与(&)运算看结果是不是1就只知道了,这个方法的问题在于对于负数的处理会导致死循环,如果是负数,则右移会在首位补1,数字永远不会变为0,最后变为0xffffffff导致死循环;常规解法 :为了避免死循环,可以不右移 输入的数字n,而转为左移 用来校验的数字1,依次校验数字n的每一位是否为1;常规解法的代码实现:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 #include <iostream> int number_of_1 (int num) int count = 0 ; unsigned int flag = 1 ; while (flag) { if (num & flag) { count++; } flag = flag << 1 ; } return count; } int main () std ::cout << number_of_1(255 ) << std ::endl ; std ::cout << number_of_1(-1 ) << std ::endl ; return 0 ; }
令人惊喜的解法 :先分析一下把一个数减去1的情况,如果一个整数不等于0,则二进制中至少有一位是1 ,假设这个数最右边为1,则减1导致最后一位为0,其余位保持不变;假设最后一位是0,如果最右边的1位于第m位,则减一时,第m位由1变0,m位之后的所有0都变成1,m之前的所有位保持不变。根据这两种情况,可以发现把一个整数减1,都是把最右边的1变成0,如果右边有0,则所有0变成1,如果把一个整数 和它减去1的结果 做位与运算 ,相当于把最右边的1变成0。以1100为例,减1结果是1011,1100和1011做位运算,结果是1000,即相比于1100把最右边的1变成0。所以最后的思路是,把一个整数减1,再和原整数做与运算,就把最右边1变为0,那么一个二进制中有多少1就可以进行多少次这样的操作。完整代码实现:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 #include <iostream> int number_of_1_sp (int num) int count = 0 ; while (num) { count++; num = (num - 1 ) & num; } return count; } int main () std ::cout << number_of_1_sp(255 ) << std ::endl ; std ::cout << number_of_1_sp(-1 ) << std ::endl ; return 0 ;