发表更新剑指Offer21 分钟读完 (大约3085个字)

《剑指Offer》第4章笔记 解题的思路 P2

一眼看不出问题的隐藏规律时，说不定能通过举例来发现。

1、2 章节

包含面试题27-29。

请到《第4章笔记 解题的思路 P1》阅读这部分内容。

3 举例让抽象问题具体化

和上一节画图的方法一样，我们也可以借助举例模拟的方法来思考分析复杂的问题。当一眼看不出问题中隐藏的规律时，可以试着用一两个具体的例子模拟操作的过程，说不定能通过具体的例子找到抽象的规律。

具体的例子也可以帮助我们向面试官解释算法思路，也能帮助我们确保代码的质量，举出来的例子可以当作测试用例检验代码的正确性。

面试题 30-34

面试题30：包含min函数的栈。

定义栈的数据结构，在该类型中实现一个能够得到栈的最小元素的min函数，在该栈中，调用min、push、pop的时间复杂度都是O(1)。

这道题容易曲解成是对这一组元素的排序，就容易陷入到一个思维陷阱，开始怀疑是怎么在O(n)时间内做到对这些元素的排序的（常用的排序也需要O(nlogn)的时间），其实多举几个例子可以发现，这个过程并不完全等价于是对一组元素的排序，栈的min值是有条件性的，取决于栈中到底有什么样的元素，以及这些元素的入栈顺序，所以用一个相同长度的栈，来存储一个元素入栈后，栈的min值是多少，就可以同步地在O(1)时间里实现min的获取。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
#include <iostream>

const int max_len = 100;

struct MinStack {
    int stack[max_len];
    int min_stack[max_len];
    int anchor = -1;

    void push(int elem) {
        if(anchor < max_len - 1) {
            stack[anchor + 1] = elem;
            if(anchor == -1 || min_stack[anchor] > elem) {
                min_stack[anchor + 1] = elem;
            } else {
                min_stack[anchor + 1] = min_stack[anchor];
            }
            anchor++;
        } else {
            // throw error
        }
    }

    int pop() {
        if(anchor >= 0) {
            anchor--;
            return stack[anchor + 1];
        } else {
            // throw error
            return - 1;
        }
    }

    int min() {
        if(anchor >= 0) {
            return min_stack[anchor];
        } else {
            // throw error
            return -1;
        }
    }
};

int main() {
    MinStack min_stack;
    for(int i = 0; i < 4; i++) {
        min_stack.push(4 - i);
        printf("After push %d, min=%d\n", 4 - i, min_stack.min());
    }
    // After push 4, min=4
    // After push 3, min=3
    // After push 2, min=2
    // After push 1, min=1
    for(int i = 0; i < 4; i++) {
        int pop = min_stack.pop();
        printf("After pop %d, min=%d\n", pop, min_stack.min());
    }
    // After pop 1, min=2
    // After pop 2, min=3
    // After pop 3, min=4
    // After pop 4, min=-1
}

面试题31：栈的压入、弹出序列。

输入两个整数序列，第一个序列表示栈的压入顺序，请判断第二个序列是否为该栈的弹出顺序。假设压入栈的所有数字均不相等，例如{1,2,3,4,5}是某栈的压栈序列，序列{4,5,3,2,1}是该栈的对应一个弹出序列，但{4,3,5,1,2}就不可能是该压栈的弹出序列。

PS：题目其实说的蛮含糊的，只要理解一个关键点就好了，它指的是执行一系列压栈和弹出操作，并不是先只压栈然后再只弹出，所以一个入栈顺序为{1,2,3,4,5}，出栈顺序也可能是{1,2,3,4,5}（进一个就出一个）。

比较直观的方法就是用一个栈来模拟整个流程，看这个流程是否能匹配上压栈和弹出的顺序。

每次压栈结束后，就检查剩余的出栈顺序，如果下一个出栈的元素就栈顶的元素就出栈，并且循环检查，直到无法再出栈。如果入栈都结束后，出栈顺序或者栈内不为空，则表示出栈顺序有错误。

完整实现代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include <iostream>
#include <stack>

bool is_pop_order(const int* ppush, const int* ppop, int len) {
    bool possible = false;
    if(ppush != nullptr && ppop != nullptr && len > 0) {
        const int* pnext_push = ppush;
        const int* pnext_pop = ppop;

        std::stack<int> stack;

        while(pnext_pop - ppop < len) {
            while(stack.empty() || stack.top() != *pnext_pop) {
                // 元素压栈
                if(pnext_push - ppush == len) {
                    break; // 元素全部已入栈
                }
                stack.push(*pnext_push);
                pnext_push++;
            }
            while(!stack.empty() && stack.top() == *pnext_pop) {
                // 元素出栈
                stack.pop();
                pnext_pop++;
            }
            if(pnext_push - ppush == len && pnext_pop - ppop != len) {
                // 入栈已空，但出栈还未空，不是正确的出栈顺序
                break;
            }
        }
        if(stack.empty() && pnext_pop - ppop == len) {
            possible = true;
        }
    }
    return possible;
}

void test(const int* ppush, const int* ppop, int len) {
    printf("%s\n", is_pop_order(ppush, ppop, len)?"yes":"no");
}

int main() {
    int push_order[5] = {1,2,3,4,5};
    int pop_order1[5] = {4,5,3,2,1};
    int pop_order2[5] = {4,3,5,1,2};
    int pop_order3[5] = {1,2,3,4,5};
    int pop_order4[5] = {5,4,3,2,1};
    test(push_order, pop_order1, 5); // yes
    test(push_order, pop_order2, 5); // no
    test(push_order, pop_order3, 5); // yes
    test(push_order, pop_order4, 5); // yes
    return 0;
}

面试题32：从上到下打印二叉树。

题目一：不分行从上到下打印，同一层按照从左到右的顺序打印，节点定义：

1
2
3
4
5
struct node {
    int value;
    node* pleft;
    node* pright;
}

思路就是之前有提到过的层序遍历了，使用队列的数据结构来辅助遍历。

打印顺序：8,6,10,5,7,9,11

完整实现代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include <iostream>
#include <queue>

struct node {
    int value;
    node* pleft;
    node* pright;
};

node* init_node(int value) { ... }
node* init_tree() { ... }

void level_order_traversal(node* proot) {
    if(proot == nullptr) {
        return;
    }
    std::queue<node*> q;
    q.push(proot);
    node* pnode;
    while(!q.empty()) {
        pnode = q.front();
        printf("%d ", pnode->value);
        if(pnode->pleft != nullptr) {
            q.push(pnode->pleft);
        }
        if(pnode->pright != nullptr) {
            q.push(pnode->pright);
        }
        q.pop();
    }
}

int main() {
    node* proot = init_tree();
    level_order_traversal(proot);
    return 0;
}

PS：书上代码用的队列是deque双端队列，不是很明白作者的用意，这里我就直接用普通队列queue了。

题目二：分行从上到下打印二叉树，每一层打印到一行，例如：

1
2
3
8
6 10
5 7 9 11

队列除了保存节点顺序，还要保存一个层数，在题目一代码基础上进行稍微的修改。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#include <iostream>
#include <queue>
#include <utility> // use std::pair
#include <tuple> // use std::tie

struct node {
    int value;
    node* pleft;
    node* pright;
};

node* init_node(int value) { ... }
node* init_tree() { ... }

void level_order_traversal(node* proot) {
    if(proot == nullptr) {
        return;
    }
    std::queue<std::pair<node*, int>> q;
    q.push(std::make_pair(proot, 1));
    node* pnode;
    int level;
    int last_level = 1;
    while(!q.empty()) {
        std::tie(pnode, level) = q.front();
        if(level > last_level) {
            printf("\n");
            last_level = level;
        }
        printf("%d\t", pnode->value);
        if(pnode->pleft != nullptr) {
            q.push(std::make_pair(pnode->pleft, level + 1));
        }
        if(pnode->pright != nullptr) {
            q.push(std::make_pair(pnode->pright, level + 1));
        }
        q.pop();
    }
}

int main() {
    node* proot = init_tree();
    level_order_traversal(proot);
    return 0;
}

书上代码把逻辑拆分的有点复杂，不够简洁，所以就用自己的方式来写了，在队列的节点中嵌入了节点的层数，用一个变量last_level来保存上一次打印节点的层数，如果发现已经到了下一层，就先输出一个换行，逻辑上更加简洁。

题目三：之字形打印二叉树，第一行按照从左到右顺序，第二行按照从右到左顺序，第三行从左到右，依次类推。

可以简单地理解为，奇数行照常顺序打印，而偶数行需要逆向打印，所以可以简单地给偶数行添加一个栈结构，先全部压栈，再出栈打印，其他流程照旧，即可实现题目的要求，在题目二的代码基础上稍加修改即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
#include <iostream>
#include <queue>
#include <utility>
#include <tuple>
#include <stack>

struct node {
    int value;
    node* pleft;
    node* pright;
};

node* init_node(int value) { ... }
node* init_tree() { ... }

void level_order_traversal_zigzag(node* proot) {
    if(proot == nullptr) {
        return;
    }
    std::queue<std::pair<node*, int>> q;
    std::stack<int> print_stack;
    q.push(std::make_pair(proot, 1));
    node* pnode;
    int level;
    int last_level = 1;
    while(!q.empty()) {
        std::tie(pnode, level) = q.front();
        if(level > last_level) {
            if(level & 0x1 == 1) {
                while(!print_stack.empty()) {
                    printf("%d\t", print_stack.top());
                    print_stack.pop();
                }
            }
            printf("\n");
            last_level = level;
        }
        if(level & 0x1 == 1) {
            // 奇数行直接输出
            printf("%d\t", pnode->value);
        } else {
            // 偶数行先压栈
            print_stack.push(pnode->value);
        }
        if(pnode->pleft != nullptr) {
            q.push(std::make_pair(pnode->pleft, level + 1));
        }
        if(pnode->pright != nullptr) {
            q.push(std::make_pair(pnode->pright, level + 1));
        }
        q.pop();
    }
    // 最后一层是偶数层时， 需要继续清空输出
    while(!print_stack.empty()) {
        printf("%d\t", print_stack.top());
        print_stack.pop();
    }
}

int main() {
    node* proot = init_tree();
    level_order_traversal_zigzag(proot);
    return 0;
}

书上的代码逻辑稍微复杂一点，要用两个栈来完成两层的循环之字输出，理解起来稍微比较难，所以我就只是简单地在题目二的基础上进行修改了，逻辑上理解起来更加方便。

面试题33：二叉搜索树的后序遍历序列。

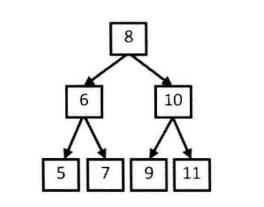
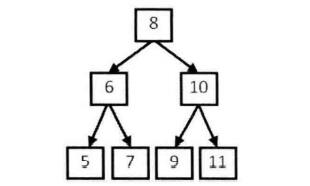
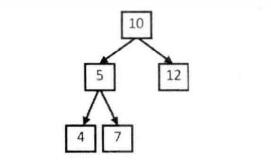
输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历结果。如果是则返回true，否则返回false。假设输入的数组的任意两个数字互不相同，如，{5,7,6,9,11,10,8}，则返回true，因为整数序列是下图的二叉搜索树的后序遍历结果，如果输入{7,4,6,5}，则返回false，无法找到这样的二叉搜索树。

后序遍历的特点在于最后访问根节点，所以对于一个树（或子树）的后续遍历序列，根节点都是最后一个数，另外，对于二叉搜索树的一个节点，其左子树的节点都小于该节点，右子树的节点都大于该节点，在遍历序列上体现就是前一部分大于节点值，后一部分小于节点值。所以解题的思路就是递归地去分解后续遍历序列，不断的去验证各个节点子树对应的后续遍历是否满足二叉搜索树的特性即可。

完整实现代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
#include <iostream>

bool is_post_order(int sequence[], int start, int end) {
    if(sequence == nullptr || start > end) {
        return false;
    }
    if(start == end) {
        return true;
    }
    int pstart, pend;
    for(pstart = start; pstart < end; pstart++) {
        if(sequence[pstart] > sequence[end]) {
            pstart--;
            break;
        }
    }
    for(pend = end - 1; pend >= start; pend--) {
        if(sequence[pend] < sequence[end]) {
            pend++;
            break;
        }
    }
    if(pstart == pend) {
        // 全偏树，此时所有节点都大于或小于子树根节点
        return is_post_order(sequence, start, end-1);
    } else if(pstart + 1 == pend) {
        // 左子树都小于节点，右子树都大于节点
        bool bleft = is_post_order(sequence, start, pstart);
        bool bright = is_post_order(sequence, pend, end-1);
        return bleft && bright;
    } else {
        // 不满足要求
        return false;
    }
}

void test(int sequence[], int start, int end) {
    printf("%s\n", is_post_order(sequence, start, end)?"yes":"no");
}

int main() {
    int sequence1[] = { 5,6,7,9,11,10,8 };
    int sequence2[] = { 7,4,6,5 };
    test(sequence1, 0, 6); // yes
    test(sequence2, 0, 3); // no
    return 0;
}

比较细致地考虑的话，要记得把全偏树的情况考虑到，此时根节点前面的所有节点都属于一个子树，而不是还是分左子树和右子树。

面试题34：二叉树中和为某一值的路径。

输入一棵二叉树和一个整数，打印出二叉树中节点值的和为输入整数的所有路径。从树的根节点开始往下一直到叶节点所经过的节点形成一条路径。二叉树节点的定义如下：

1
2
3
4
5
struct node {
    int value;
    node* pleft;
    node* pright;
}

和为22的路径有两条，10、5、7和10、12

直观的方法应该就是递归地往下遍历所有情况，到叶节点的时候计算路径上的节点和，如果和等于输入的整数，则输出路径。

完整实现代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include <iostream>
#include <vector>

struct node {
    int value;
    node* pleft;
    node* pright;
};

node* init_node(int value) { ... }
node* init_tree() { ... }

std::vector<node*> path; // 存储路径

void find_path(node* pnode, int sum, int expect_sum) {
    if(pnode == nullptr) {
        return;
    }
    if(pnode->pleft == nullptr && pnode->pright == nullptr
        && sum + pnode->value == expect_sum) {
        // 满足要求，输出节点
        path.push_back(pnode);
        for(int i = 0; i < path.size(); i++) {
            printf("%d ", path[i]->value);
        }
        printf("\n");
        path.pop_back();
        return;
    }
    path.push_back(pnode);
    if(pnode->pleft != nullptr) {
        find_path(pnode->pleft, sum + pnode->value, expect_sum);
    }
    if(pnode->pright != nullptr) {
        find_path(pnode->pright, sum + pnode->value, expect_sum);
    }
    path.pop_back();
}

int main() {
    node* tree = init_tree();
    find_path(tree, 0, 22);
    return 0;
}

这道题可能会联想到提前剪枝的优化，例如当还没有到叶节点时，发现和已经大于了期望值的和，此时提前停止往下查询的操作叫做剪枝，但需要注意的是本题目中并没有限定节点的值value一定是正数(类型也是int而非unsigned int)，可以出现途中和大于期望值和，所以本题不能用这样的剪枝优化方法。

4 分解让复杂问题简单化

包含面试题35-38。

请到《第4章笔记 高质量代码 P3》阅读这部分内容。

《剑指Offer》第4章笔记 解题的思路 P2

https://yumi-cn.github.io/2021/01/02/s2o-c4-part2/

作者

Yumiko

发布于

2021-01-02

更新于

2021-01-02

许可协议

#

喜欢这篇文章？打赏一下作者吧

评论

关注我

专栏

最新文章

×