《剑指Offer》第4章笔记 解题的思路 P3

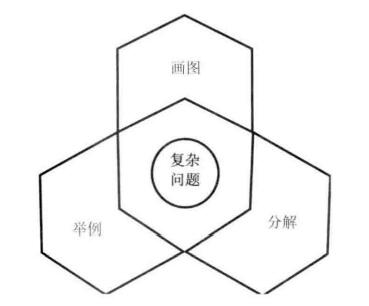
遇到复杂的问题，可以尝试将大问题分解为若干小问题。

1、2 章节

包含面试题27-29。

请到《第4章笔记 解题的思路 P1》阅读这部分内容。

3 章节

包含面试题30-34。

请到《第4章笔记 高质量代码 P2》阅读这部分内容。

4 分解让复杂问题简单化

在面试中，当我们遇到复杂的大问题的时候，如果能够先把大问题分解成若干个简单地小问题，然后再逐个解决这些小问题，则可能也会容易很多。

在计算机领域有一类算法叫分治法，即“分而治之”，把分解后的小问题各个解决，然后把小问题的解决方案结合起来解决大问题。

面试题35-38

面试题35：复杂链表的复制。

实现函数ComplexListNode* clone(ComplexListNode* phead)，复制一个复杂链表。在复杂链表中，每个节点除了有一个pnext指针指向下一个节点，还有一个psibling指针指向链表中的任意节点或者nullptr。节点定义如下：

struct ComplexListNode {
    int value;
    ComplexListNode* pnext;
    ComplexListNode* psibling;
};

1. 直观地思路是先复制整个链表，然后使用一个辅助存储空间来存储节点间的映射关系，例如用一个哈希表来存储<节点、克隆节点>的映射关系，这样在建立psibling关系时十分有用，时间开销也可以做到O(n)；
2. 进一步地，可以不用借助辅助的空间来存储节点对应关系，例如直接先将克隆节点挂靠在原节点后面，用这种方式来替代哈希表，同时也可以方便地建立psibling关系，这种方法对应的缺陷是过程中会对原数据结构进行修改，如果外部程序允许，则可以这样操作（在一些并行程序中可能会出现问题）。

完整实现代码：

#include <iostream>

struct ComplexListNode {
    int value;
    ComplexListNode* pnext;
    ComplexListNode* psibling;
};

ComplexListNode* init_node(int value) { ... }
ComplexListNode* init_list() { ... }

ComplexListNode* clone(ComplexListNode* phead) {
    if(phead == nullptr) {
        return nullptr;
    }
    ComplexListNode* pnode = phead;
    // 克隆节点
    while(pnode != nullptr) {
        ComplexListNode* pclone = init_node(pnode->value);
        pclone->pnext = pnode->pnext;
        pnode->pnext = pclone;
        pnode = pclone->pnext;
    }
    pnode = phead;
    // 建立克隆节点的sibling关系
    while(pnode != nullptr) {
        if(pnode->psibling != nullptr) {
            ComplexListNode* psibling = pnode->psibling;
            ComplexListNode* pclone = pnode->pnext;
            pclone->psibling = psibling->pnext;
        }
        pnode = pnode->pnext->pnext;
    }
    ComplexListNode* pclone_head = nullptr;
    ComplexListNode* ptemp = nullptr;
    pnode = phead;
    // 从链表中分离出克隆节点
    while(pnode != nullptr) {
        if(pclone_head == nullptr) {
            pclone_head = pnode->pnext;
        } else {
            ptemp->pnext = pnode->pnext;
        }
        ptemp = pnode->pnext;
        pnode->pnext = ptemp->pnext;
        ptemp->pnext = nullptr;
        pnode = pnode->pnext;
    }
    return pclone_head;
}

void print(ComplexListNode* phead) {
    ComplexListNode* pnode = phead;
    while(pnode != nullptr) {
        printf("%d", pnode->value);
        if(pnode->psibling != nullptr) {
            printf("->%d", pnode->psibling->value);
        }
        printf("\n");
        pnode = pnode->pnext;
    }
}

int main() {
    ComplexListNode* phead = init_list();
    ComplexListNode* pclone = clone(phead);
    print(phead);
    print(pclone);
    return 0;
}

---

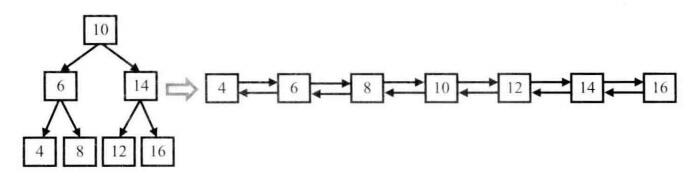
面试题36：二叉搜索树与双向链表。

输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的双向链表。要求不能创建任何新的节点，只能调整树中节点指针的指向。比如，输入图4.15中左边的二叉搜索树，则输出转换之后的排序双向链表。二叉树节点定义如下：

struct node {
  int value;
  node* pleft;
  node* pright;
};

稍微观察就可以发现，对于单个的一个节点（子树），转换为双向链表时，只需要将其左子树的最大节点和其右子树的最小节点传分别链接到两个对应指针上，递归地处理其左子树和右子树，就可以得到最终的结果。

完整实现代码：

#include <iostream>

struct node {
    int value;
    node* pleft;
    node* pright;
};

node* init_node(int value) { ... }
node* init_tree() { ... }

void tree_to_list_core(node* proot, node** max, node** min) {
    if(proot == nullptr) {
        return;
    }
    node *lmax, *lmin, *rmax, *rmin;
    lmax = lmin = rmax = rmin = nullptr;
    tree_to_list_core(proot->pleft, &lmax, &lmin);
    tree_to_list_core(proot->pright, &rmax, &rmin);
    *max = rmax?rmax:proot; // 确定头节点(最小节点)
    *min = lmin?lmin:proot; // 确定尾节点(最大节点)
    if(lmax != nullptr) {
        lmax->pright = proot;
    }
    proot->pleft = lmax;
    if(rmin != nullptr) {
        rmin->pleft = proot;
    }
    proot->pright = rmin;
}

void tree_to_list(node* proot, node** max, node** min) {
    if(proot == nullptr) {
        return;
    }
    tree_to_list_core(proot, max, min);
}

void dual_print(node* phead, node* ptail) {
    // 顺序打印
    node* pnode = phead;
    printf("Min -> Max: ");
    while(pnode != nullptr) {
        printf("%d ", pnode->value);
        pnode = pnode->pright;
    }
    printf("\n");
    // 逆序打印
    pnode = ptail;
    printf("Max -> Min: ");
    while(pnode != nullptr) {
        printf("%d ", pnode->value);
        pnode = pnode->pleft;
    }
    printf("\n");
}

int main() {
    node* proot = init_tree();
    node *phead, *ptail;
    phead = ptail = nullptr;
    tree_to_list(proot, &ptail, &phead);
    dual_print(phead, ptail);
    return 0;
}

书上使用的方法是，在中序遍历的同时，在函数参数中加上一个已构建链表的尾节点，逐步地向尾部挂链节点，这样的方法个人逻辑上理解起来有点绕，所以我自己写的时候，对函数的定义是要同时确定重构建链表的头节点和尾节点，这样逻辑构建上感觉会更加清晰一点，并且最后可以直接返回双向链表的头节点和尾节点，无需再去重新遍历寻找，核心算法的时间效率上和书上代码并没有太大区别。

---

面试题37：序列化二叉树。

请实现两个函数，分别用来序列化和反序列化二叉树。

PS：序列化(Serialization)指的是将对象的状态信息转换为可以存储或传输的形式的过程，反序列化则是通过序列化信息来重建对应状态的对象。

之前的面试题7“重建二叉树”，我们知道可以从前序遍历和中序遍历构造出一棵（也是唯一的）二叉树。受启发，可能可以尝试把一棵二叉树序列化成一个前序和一个中序，然后反序列通过两个序列重构出原二叉树。

但这样的思路有两个问题：

1. 这种方法要求二叉树不能有数值重复的节点（如果有重复的节点，在确定根节点时会出现歧义）；
2. 只有两个序列中所有数据都读出来后才能开始反序列化，如果两个遍历数据只能从一个流中读取，那么可能要等待较长时间。

实际上，如果二叉树的序列化是从根节点开始的，那么相应的反序列化在根节点的数值读出来的时候就可以开始了。因此，可以根据前序遍历的顺序来序列化二叉树，在二叉树碰到nullptr时，转化为一个特殊的字符(比如$)，另外节点的数值要用一个特殊字符(比如,)隔开。

完整代码实现：

#include <iostream>

struct node {
    int value;
    node* pleft;
    node* pright;
};

node* init_node(int value) { ... }
node* init_tree() { ... }

void serialize(node* proot, char*& stream) {
    if(proot == nullptr) {
        *stream = '$';
        *(stream + 1) = ',';
        *(stream + 2) = '\0';
        stream += 2;
        return;
    }
    *stream = '0' + proot->value;
    *(stream + 1) = ',';
    *(stream + 2) = '\0';
    stream += 2;
    serialize(proot->pleft, stream);
    serialize(proot->pright, stream);
}

bool read_stream(char*& stream, int* number) {
    if(*stream <= '9' && *stream >= '0') {
        *number = *stream - '0';
        stream += 2;
        return true;
    } else {
        stream += 2;
        return false;
    }
}

void deserialize(node** proot, char*& stream) {
    int number;
    if(read_stream(stream, &number)) {
        *proot = init_node(number);
        deserialize(&((*proot)->pleft), stream);
        deserialize(&((*proot)->pright), stream);
    }
}

void preorder_traversal(node* proot) {
    if(proot == nullptr) {
        return;
    }
    printf("%d ", proot->value);
    preorder_traversal(proot->pleft);
    preorder_traversal(proot->pright);
}

int main() {
    node* proot = init_tree();
    char* stream = new char[100];
    char* pchar = stream;
    serialize(proot, pchar);
    printf("%s\n", stream);
    node* new_proot = nullptr;
    pchar = stream;
    deserialize(&proot, pchar);
    preorder_traversal(proot);
    return 0;
}

这里利用了先序遍历的节点顺序特性，使用中序或者后序就无法实现这样的效果，算是一种特殊的技巧吧，用$替代空指针nullptr，在先序遍历的同时确定之后重建的顺序。序列化中一些需要注意的细节，比如使用的替代字符$是否在节点value范围中，要使用间隔符,将值隔开，避免节点值产生混淆错误。

---

面试题38：字符串的排列。

输入一个字符串，打印出该字符串中字符的所有排列。例如，输入字符串abc，则打印由字符a、b、c所能排列出的所有字符串abc、acb、bac、bca、cab和cba。

基础思路是使用递归来完成，例如确定一个字符后，只需要知道剩下字符串的全排列即可，在第i层递归时，从还未选择的字符中确定一个字符在输出的第i个位置，遍历所有可能性，也就是全排列的实现方式。

完整实现代码：

#include <iostream>
#include <cstring>

void permutation(char* string, bool* choose, int len, char* output, int olen) {
    if(olen == len) {
        *(output + olen) = '\0';
        printf("%s\n", output);
    }
    for(int i = 0; i < len; i++) {
        if(!choose[i]) {
            *(output + olen) = string[i];
            choose[i] = true;
            permutation(string, choose, len, output, olen + 1);
            choose[i] = false;
        }
    }
}

void permutation(char* string) {
    if(string == nullptr) {
        return;
    }
    int len = strlen(string);
    char* output = new char[len + 1];
    output[0] = '\0';
    bool* choose = new bool[len];
    memset(choose, 0, sizeof(choose));
    permutation(string, choose, len, output, 0);
}

int main() {
    char* string = "abc";
    permutation(string);
}

书上的代码是通过交换原字符串中各字符的位置来实现的，自己写代码时为了确保字符串本身不被修改，所以使用了一个bool* choose数组来记录被选中的字符位置，以及char* output来记录字符的顺序（用以最后的输出）。

5 总结

图形使抽象的问题形象化。

举例使抽象的问题具体化。

分解使复杂的问题易解化。