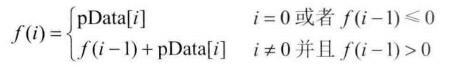发表更新剑指Offer1 小时读完 (大约12171个字)

《剑指Offer》第5章笔记 优化效率

时间与空间，是算法永恒的话题。

1 面试官谈效率

大佬们说的名言名句。

咕咕待更。

2 时间效率

面试官除了考查应聘者的编程能力，还关注应聘者有没有不断优化效率、追求完美的态度和能力。

首先，我们的编程习惯对代码的时间效率有很大影响。比如C/C++程序员要养成采用引用（或指针）传递复杂类型参数的习惯。如果采用值传递的方式，则从形参到实参会产生一次复制操作，这样的复制大部分时候是多余的，应该尽量避免。再比如，C#中做多次字符串的拼接操作，尽量不要用多次String的+运算符来拼接字符串，因为这样会产生很多String的临时实例，造成时间和空间的浪费，更好的办法是用StringBuilder的Append方法来完成字符串的拼接。如果我们平时不太注意这些影响代码效率的细节，没有养成好的编码习惯，写出的代码可能会让面试官大失所望。

其次，即使同一个算法用循环和递归两种思路实现的时间效率可能会大不一样。递归的本质是把一个大的复杂问题分解成两个或者多个小的简单问题。如果小问题有相互重叠的部分，那么直接用递归实现虽然代码显得很简洁，但时间效率可能会非常差，对于这种题目，可以用递归地思路来分析，写代码的时候可以基于循环实现，并且用数组来保存中间结果，绝大部分动态规划算法的分析和代码实现都是分这两个步骤完成的。

再次，代码的时间效率还能体现应聘者对数据结构和算法功底的掌握程度。同样是查找，如果是顺序查找则需要O(n)的时间；如果输入的是排序的数组则只需要O(logn)的时间；如果事先已经构造好了哈希表，那么查找在O(1)时间内就能完成。

最后，应聘者在面试的时候要展示敏捷的思维能力和追求完美的激情，这些对最终的面试结果也有很重要的影响。

面试题 39-48

面试题39：数组中出现次数超过一半的数字。

数组中有一个数字出现的次数超过数组长度的一半，请找出这个数字。例如，输入一个长度为9的数组{1,2,3,2,2,2,5,4,2}。由于数字2在数组中出现了5次，超过数组长度的一半，因此输出2。

解法一：基于Partition函数的时间复杂度为O(n)的算法。

数组中有一个数字出现的次数超过了数组长度的一半，如果这个数组排序，那么排序之后位于数组中间的数字，一定就是那个出现次数超过数组长度一半的数字。这个数字就是统计学上的中位数，即长度为n的数组中第n/2大的数字。我们有成熟的时间复杂度为O(n)的算法得到数组中任意第k大的数字。

这种算法受快速排序算法的启发。在随机快速排序算法中，先在数组中随机选择一个数字，然后调整数组中数字的顺序，使得比选中的数字小的数字都排在它的左边，比选中的数字大的数字都排在它的右边。如果这个选中的数字下标刚好是n/2，则这个数字就是数组的中位数；如果下标大于n/2，那么中位数应该在它的左边，接着在它的左边找；如果下标小于n/2，中位数在它的右边，接着在它的右边找。这是一个典型的递归过程。

完整实现代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
#include <iostream>

int partition(int* numbers, int len, int start, int end) {
    if(start == end) {
        return start;
    }
    int anchor = numbers[end];
    int left = start;
    int right = end - 1;
    while(left < right) {
        while(numbers[left] < anchor && left < right) {
            left++;
        }
        while(numbers[right] >= anchor && left < right) {
            right--;
        }
        if(left != right) {
            int temp = numbers[left];
            numbers[left] = numbers[right];
            numbers[right] = temp;
        }
    }
    if(left != end - 1 || numbers[left] > anchor) {
        int temp = numbers[left];
        numbers[left] = numbers[end];
        numbers[end] = temp;
    } else {
        left = end;
    }
    return left;
}

bool g_input_invalid = false;

bool check_array(int* numbers, int len) {
    g_input_invalid = false;
    if(numbers == nullptr || len <= 0) {
        g_input_invalid = true;
    }
    return g_input_invalid;
}

bool check_more_than_half(int* numbers, int len, int number) {
    int times = 0;
    for(int i = 0; i < len; i++) {
        if(numbers[i] == number) {
            times++;
        }
    }
    bool is_more_than_half = true;
    if(times * 2 <= len) {
        g_input_invalid = true;
        is_more_than_half = false;
    }
    return is_more_than_half;
}

int more_than_half_num(int* numbers, int len) {
    if(check_array(numbers, len)) {
        return 0;
    }
    int middle = len >> 1;
    int start = 0;
    int end = len - 1;
    int index = partition(numbers, len, start, end);
    while(index != middle) {
        if(index > middle) {
            end = index - 1;
            index = partition(numbers, len, start, end);
        } else {
            start = index + 1;
            index = partition(numbers, len, start, end);
        }
    }
    int result = numbers[middle];
    if(!check_more_than_half(numbers, len, result)) {
        result = 0;
    }
    return result;
}

int main() {
    int numbers[] = { 1, 2, 3, 2, 2, 2, 5, 4, 2 };
    int result = more_than_half_num(numbers, 9);
    if(g_input_invalid) {
        printf("Invalid input.\n");
    } else {
        printf("Result: %d\n", result);
    }
    return 0;
}

在面试的时候，除了完成基本功能，还要考虑一些无效的输入。如果函数的输入参数是一个指针（数组在参数传递的时候退化为指针），就要考虑这个指针可能为nullptr。代码中的check_array用来判断输入的数组是不是无效的。check_more_than_half用来检验输入的数组中，是不是这个数字出现次数大于长度一半，用全局变量g_input_invalid来表示输入无效的情况。

解法二：根据数组特点找出时间复杂度为O(n)的算法。

从另一个角度来解决这个问题。数组中有一个数字出现的次数超过数组长度的一半，也就是说它出现的次数比其他所有数字出现的和还要多。因此，考虑在遍历数组的时候保存两个值，一个是数组中的一个数字，另一个是次数。当遍历到下一个数字时，如果下一个数字和之前保存的数字相同，则次数加1；如果下一个数字和之前保存的不同，则次数减1；如果次数为0，则保存下一个数字，并把次数设1。由于要找的数字出现的次数比其他所有出现的次数之和还要多，那么要找的数字肯定是最后一次把次数设为1对应的数字。

完整实现代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include <iostream>

bool g_input_invalid = false;
bool check_array(int* numbers, int len) { ... }
bool check_more_than_half(int* numbers, int len, int number) { ... }

int more_than_half_num(int* numbers, int len) {
    if(check_array(numbers, len)) {
        return 0;
    }
    int result = numbers[0];
    int times = 1;
    for(int i = 0; i < len; i++) {
        if(times == 0) {
            result = numbers[i];
            times = 1;
        } else if(numbers[i] == result) {
            times++;
        } else {
            times--;
        }
    }
    if(!check_more_than_half(numbers, len, result)) {
        result = 0;
    }
    return result;
}

int main() {
    int numbers[] = { 1, 2, 3, 2, 2, 2, 5, 4, 2 };
    int result = more_than_half_num(numbers, 9);
    if(g_input_invalid) {
        printf("Invalid input.\n");
    } else {
        printf("Result: %d\n", result);
    }
    return 0;
}

两种解法算法的时间复杂度都是O(n)，在第一种解法中，需要交换数组中数字的顺序，这就会修改输入的数组，而在面试的时候需要尝试和面试官讨论，明确需求，如果说不能修改输入的数组，就只能采用第二种解法了。

面试题40：最小的K个数。

输入n个整数，找出其中最小的k个数，例如，输入4,5,1,6,2,7,3,8这8个数字，则最小的4个数字是1,2,3,4。

最简单直观的解法就是进行k次数组遍历，每一次找出一个相对最小值，时间复杂度O(nk)，代码比较简单就不再写了，主要讲两种优化的思路。

解法一：时间复杂度为O(n)的算法，只有当我们可以修改输入的数组时可用。

同样可以基于partition函数来解决这个问题。如果基于数组的第k个数字来调整，使得比第k个数字小的所有数字都位于数组的左边，比第k个数大的所有数字都位于数组的右边。这样，位于数组中左边的k个数字就是最小的k个数字（k个数字不一定是排序的）。

完整实现代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include <iostream>

int partition(int* numbers, int len, int start, int end) { ... }

void find_k_min(int* input, int n, int* output, int k) {
    if(input == nullptr || output == nullptr || k > n || n <= 0 || k <= 0) {
        return;
    }
    int start = 0;
    int end = n - 1;
    int index = partition(input, n, start, end);
    while(index != k - 1) {
        if(index > k - 1) {
            end = index - 1;
            index = partition(input, n, start, end);
        } else {
            start = index + 1;
            index = partition(input, n, start, end);
        }
    }
    for(int i = 0; i < k; i++) {
        output[i] = input[i];
    }
}

int main() {
    int input[] = { 4,5,1,6,2,7,3,8 };
    int n = 8;
    int k = 4;
    int* output = new int[k];
    find_k_min(input, n, output, k);
    for(int i = 0; i < k; i++) {
        printf("%d ", output[i]);
    }
    return 0;
}

如果面试官要求不能修改输入的数组，那么就只能另辟蹊径。

解法二：时间复杂度为O(nlogk)的算法，特别适合处理海量数据。

先创建一个大小为k的数据容器来存储最小的k个数字，接下来每次从输入的n个整数中读入一个数。如果容器中少于k个，则直接把这次读入的整数放入容器中；如果容器已经有k个了，此时比较读入的数字和容器中最大的数字，如果读入的更小，就插入容器，删除掉最大的。

如果用一棵二叉树（堆）来实现容器，那么就能在O(logk)时间内完成一个序列的最大值构建（O(1)的时间得到最大值，O(logk)时间完成删除和插入操作），对于n个输入数字，总的时间效率是O(nlogk)。

从头实现一个最大堆需要一定的代码，面试的几十分钟内很难完成，我们可以借助STL提供的一些数据结构，例如set或者multiset（区别是后者可以重复），如果面试官不反对使用STL，就可以直接拿来用，根据这道题的需求，使用multiset更加合适一点。

完整实现代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include <iostream>
#include <set>

// std::greater 代表递减排序 最大的在begin
typedef std::multiset<int, std::greater<int>> int_set;
typedef std::multiset<int, std::greater<int>>::iterator int_set_iter;

void find_k_min(int* input, int n, int* output, int k) {
    if(input == nullptr || output == nullptr || k > n || n <= 0 || k <= 0) {
        return;
    }
    int_set set;
    for(int i = 0; i < n; i++) {
        if(set.size() < k) {
            set.insert(input[i]);
        } else {
            int_set_iter iter = set.begin();
            if(*iter > input[i]) {
                set.erase(iter);
                set.insert(input[i]);
            }
        }
    }
    int_set_iter iter = set.begin();
    for(int i = 0; i < k; i++) {
        output[i] = *iter;
        iter++;
    }
}

int main() {
    int input[] = { 4,5,1,6,2,7,3,8 };
    int n = 8;
    int k = 4;
    int* output = new int[k];
    find_k_min(input, n, output, k);
    for(int i = 0; i < k; i++) {
        printf("%d ", output[i]);
    }
    return 0;
}

第一种基于函数partition的第一种解法平均时间复杂度是O(n)，比第二种解法要快，但同时也有限制，比如会修改输入的数组（开O(n)空间虽然可以解决，但是有额外的空间代价）。

第二种基于最大堆容器的解法虽然慢，但一是没有修改输入的数据，二是算法适合海量数据的处理，因为第二种方法不用一次性将全部数据都读入到内存中，而第一种方法只有全部读入才能计算。

面试题41：数据流中的中位数。

如何得到一个数据流的中位数？如果从数据流读出的数据是奇数个，那么中位数就是所有值排序之后位于中间的数值；如果从数据流中读取偶数个数值，那么中位数是排序之后两个数的平均值。

数据是从一个数据流中读出来的，因而数据的数目随着时间的变化而增加，如果用一个数据容器来保存从流中读出来的数据，则当有新的数据从流中读出来，这些数据就插入数据容器（所以中位数是一个不断在变化的值，和容器的状态相关）。

那么可以考虑用几种不同的数据结构来作为容器：

  • 数组：没有排序，可以使用partition找出数组的中位数，输入复杂度O(1)，找数中位数O(n)；
  • 排序数组：O(logn)时间搜索，但需要O(n)时间来插入，得到中位数的时间是O(1)；
  • 排序链表：O(n)时间插入，定义两个指针来指向链表中间的节点（不断调整的开销O(1)），所以找出中位数只需要O(1)；
  • AVL树：O(logn)时间插入一个新节点，用O(1)时间得到所有节点的中位数，虽然AVL效率很高，但是大部分编程语言的函数库都没有实现这个数据结构，自己在短时间内实现也很麻烦；
  • 最大堆+最小堆：以把中位数定义为将数组分为两个部分，前一部分小于中位数，后一部分大于中位数，所以其实我们不需要前后部分一定要完整地排序，我们只需要得到前一部分的最大值和后一部分的最小值，所以可以用最大堆来组织前一部分，用最小堆组织后一部分，让两部分的大小接近相等，插入时间O(logn)，得到中位数的时间O(1)。


基于STL中的函数push_heap、pop_heap及vector实现堆。比较仿函数less和greater分别用来实现最大堆和最小堆。

完整实现代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
#include <iostream>
#include <algorithm> // push_heap/pop_heap/less/greater
#include <vector>
#include <exception>

template<typename T> class DynamicArray {
    public:
        void insert(T num) {
            if(((min.size() + max.size()) & 1) == 0) {
                // 已经有偶数个，但有可能是0
                if(max.size() > 0 && num < max[0]) {
                    // 如果这个数比最大堆的堆顶元素小，要先放进最大堆
                    max.push_back(num);
                    // 构建堆
                    std::push_heap(max.begin(), max.end(), std::less<T>());
                    // 拿出堆顶元素
                    num = max[0];
                    // pop_head，将堆顶元素放在后面
                    std::pop_heap(max.begin(), max.end(), std::less<T>());
                    // 元素出堆
                    max.pop_back();
                }
                // 元素进最小堆
                min.push_back(num);
                std::push_heap(min.begin(), min.end(), std::greater<T>());
            } else {
                // 已经有奇数个
                if(min.size() > 0 && min[0] < num) {
                    // 如果这个数比最小堆的堆顶元素大，要先放进最小堆
                    min.push_back(num);
                    // 构建堆
                    std::push_heap(min.begin(), min.end(), std::greater<T>());
                    // 拿出堆顶元素
                    num = min[0];
                    // 堆顶元素放在后面
                    std::pop_heap(min.begin(), min.end(), std::greater<T>());
                    // 元素出堆
                    min.pop_back();
                }
                // 元素进最大堆
                max.push_back(num);
                std::push_heap(max.begin(), max.end(), std::less<T>());
            }
        }

        T get_median() {
            int size = min.size() + max.size();
            if(size == 0) {
                // throw error
                std::logic_error ex("Empty!");
                throw std::exception(ex);
            }
            T median = 0;
            if((size & 1) == 1) {
                median = min[0]; // 偶数的时候进最小堆，所以奇数时最小堆会多一个
            } else {
                median = (min[0] + max[0]) / 2;
            }
            return median;
        }

    private:
        std::vector<T> min;
        std::vector<T> max;
};

void stream_median(int* stream, int n) {
    if(stream == nullptr || n <= 0) {
        return;
    }
    DynamicArray<int> darray; // 注意模板类的声明使用方法
    for(int i = 0; i < n; i++) {
        darray.insert(stream[i]);
        printf("Read index=%d, median=%d\n", i, darray.get_median());
    }
}

int main() {
    int stream[] = { 1,2,3,4,5,6,7,8,9,10,0,1,2,3,4,5,6,7,8,9};
    stream_median(stream, 20);
    return 0;
}

其中使用到了代码里不常用的模板类，如果面试题有说明具体的数据类型，也可以直接用那个数据类型，而不是使用模板类。

其中使用到的几个和堆相关的函数进行一下说明，以后可能会用到：

  • make_heap(begin, end, comp)：虽然在这里没有用到，但还是说明一下，将一个数组(vector)的指定部分([begin,end))进行堆排序，堆顶元素放在第一个位置，默认使用的comp是less<T>，即最大元素放在第一个位置（最大堆），greater<T>为最小元素放在第一个位置（最小堆）；
  • push_heap(begin, end, comp)：一般在调用前，把一个新元素放在数组的尾部(vec.push_back(elm))，然后再调用函数对插入尾部的元素做堆排序；
  • pop_heap(begin, end, comp)：将堆顶元素移动到数组尾部，同时将剩下的元素重新构造成堆结构；
  • sort_heap(begin, end, comp)：将一个堆做排序，最终成为一个有序的序列，前提条件是输入的数组范围本身是一个对应comp的堆，如果comp是less<T>，最大堆最终序列是一个递增序列（大的在后面），如果是greater<T>，最小堆最终序列是一个递减序列（小的在后面）；

面试题42：连续子数组的最大和。

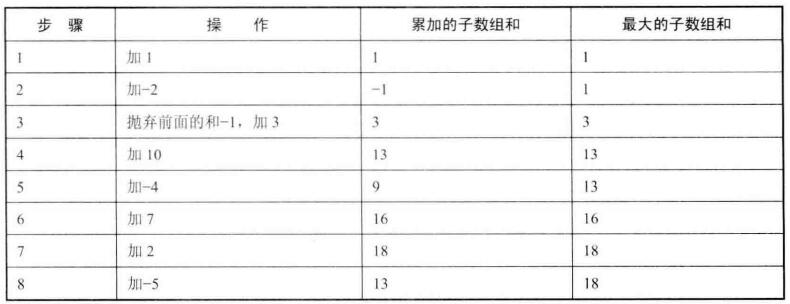
输入一个整型数组，数组里有正数也有负数。数组中的一个或连续多个整数组成一个子数组。求所有子数组的和的最大值（就是和最大的那个子数组的和值是多少），要求时间复杂度O(n)；例如，输入的数组为{1,-2,3,10,-4,7,2,-5}，和最大的子数组为{3,10,-4,7,2}，因此输出为该子数组的和18。

最简单直观的暴力遍历法就不说了（时间O(n^2)），只说优化的解决方案。

解法一：举例分析数组的规律。

从头开始往后加可以分析其中的规律，例如从某一步从i开始向后累加和，到j之前如果和已经为负数了，那么对于j而言，如果再加上前面这前j-i个位置的数字肯定不会比j自身要大，所以要计算从j开始的可能最大子数组和，就不用再加上前j-i位置的数字，重新从j开始求子数组和；同时求和的过程中，不断的更新记录的最大和。

计算数组{1,-2,3,10,-4,7,2,-5}中最大子数组和的过程

完整实现代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include <iostream>
#include <limits.h> // INT_MIN INT_MAX

bool g_invalid_input = false;

bool check_input(int* data, int len) {
    g_invalid_input = false;
    if(data == nullptr || len <= 0) {
        g_invalid_input = true;
        return false;
    } else {
        return true;
    }
}

int find_max_sub_sum(int* data, int len) {
    if(!check_input(data, len)) {
        return 0;
    }
    int max_sum = INT_MIN;
    int sum = 0;
    for(int i = 0; i < len; i++) {
        if(sum < 0) {
            sum = 0;
        }
        sum += data[i];
        if(max_sum < sum) {
            max_sum = sum;
        }
    }
    return max_sum;
}

int main() {
    int data[] = {1, -2, 3, 10, -4, 7, 2, -5};
    int result = find_max_sub_sum(data, 8);
    if(g_invalid_input) {
        printf("Invalid input.\n");
    } else {
        printf("Max sum: %d\n", result); // 18
    }
    return 0;
}

解法二：动态规划法。

如果用函数f(i)表示以第i个数字结尾的子数组（即必须包含这个尾元素）的最大和，那么我们需要求出max{f(i)}, 0<=i<=n，可以用如下递归公式来求f(i)：

其实公式的意义和解法一的思路是相同的，不过表达形式不同，代码就不再写一遍了。

面试题43：1~n整数中1出现的次数。

输入一个整数n，求1~n这n个整数的十进制表示中1出现的次数，例如，输入12，1~12这些整数中包含1的数字有1、10、11和12，1一共出现了5次。

简单地方法就不再写了，主要写一下书上的优化方法（其实还蛮不好理解的），直接看书上举的例子吧。

  • 例如1~21345，首先拆成1~1345和1346~21345，前者可以递归地调用1~n；
  • 1346~21345必然会包含10000~19999（因为21345的顶位2大于1），所以顶位上出现的1的个数有10^4个；如果定位小于1，即只包括1346~11345或者说10000~11345这部分，顶位的1个数就只有1346+1个；
  • 1346~21345数完顶位后，开始计数其他位的1个数，此时分为两组1346~11345,11346~21345，这样分的目的是，1346~11345的后4位x1346~x1345整好覆盖了4位数的所有情况0~9999，所以只需要其中一位固定1，其他位任选0~9，就可以得到该位上的1个数，所以对于一组1346~11345有4*10^3个，11346~21345同理4*10^3个，所以一共2*4*10^3个；
  • 最后将递归求解的1~1345计数，和1346~21345顶位计数和其他位技术相加，就得到最后的结果。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
#include <iostream>
#include <cstring>

int pow_base_10(unsigned int n) {
    int result = 1;
    for(unsigned int i = 0; i < n; i++) {
        result *= 10;
    }
    return result;
}

int count_1(const char* str_n) {
    if(!str_n || *str_n < '0' || *str_n > '9' || *str_n == '\0') {
        return 0;
    }
    int first = *str_n - '0';
    unsigned int len = (unsigned int)strlen(str_n);
    if(len == 1 && first == 0) {
        return 0;
    }
    if(len == 1 && first > 0) {
        return 1;
    }

    // 假设str_n是 21345
    // num_first_digit 是数字10000~19999的第一位中的数目
    int num_first_digit = 0;
    if(first > 1) {
        // 无论first有多大，只要大于1
        // 就包含10000~19999这些数（目前的例子下）
        // 所以目前的顶位出现的1的数量有 10^(len-1)个
        num_first_digit = pow_base_10(len - 1);
    } else if(first == 1) {
        // 如果fisrt位1，就是10000~11345这种情况
        // 这个时候就有1345+1个1出现在顶位上
        num_first_digit = atoi(str_n + 1) + 1;
    }
    // 1346~21345除了在顶位之外的数位上1的情况
    // 最高位是2，所以分成两段 1346~11345 11346~21345
    // 每一段剩下的4位数字中，选择其中一位是1，其余三位可以在0~9数字中选择
    // 根据排列组合有 2 * 4 * 10^3
    int num_other_digit = first * (len - 1) * pow_base_10(len - 2);
    // 1~1345的1的数目
    int num_rec = count_1(str_n + 1);
    return num_first_digit + num_other_digit + num_rec;
}

int count_1_from_1_to_n(int n) {
    if(n < 1) {
        return 0;
    }
    char str_n[50];
    sprintf(str_n, "%d", n);
    return count_1(str_n);
}

int main() {
    printf("1~%d have %d '1'\n", 12, count_1_from_1_to_n(12));
    printf("1~%d have %d '1'\n", 21345, count_1_from_1_to_n(21345));
    return 0;
}

最基础的思路需要O(nlogn)的时间，优化后的思路只需要O(logn)，所以要快得多。

面试题44：数字序列中某一位的数字。

数字以0123456789101112131415...的格式，序列化到一个字符序列中。在这个序列中，第5位(从0开始计数)是5，第13位是1，第19位是4，等等。写一个函数，求任意第n位对应的数字。

直接的方法就是从0开始逐一地枚举每个数组，每枚举一个数字时，求该数字是几位数，并把位数累加，如果位数只和小于或等于输入的n，则继续枚举下一个数字，当累加位数大于n时，第n位数字一定在这个数字里，我们再从该数字中找出对应的一位。

这样的方法还不够优化，其实是可以有规律地一段段跳过的，例如寻找第1001位：

  • 0~9一共10个字符，1001>10，在后面的字符中寻找第991位；
  • 10~99一共180(90*2)个字符，991>180，在后面的字符中寻找第881位；
  • 100~999一共2700(900*3)个字符，881<2700，所以第n位一定是100~999中间的某个数，由于811=270*3+1，意味着第881位是从100开始的第270个数字(370)的中间1位，即7。

完整代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
#include<iostream>
#include<cmath> // std::pow

// 得到为m位数字总共有多少个
// 例如m=2，返回(10~99)一共90个
// m=3，返回(100~999)一共900个
int count_of_integers(int digits) {
    if(digits == 1) {
        return 10;
    }
    int count = (int) std::pow(10, digits - 1);
    return 9 * count;
}

// 得到在m位数字中，第一个数字
int begin_num(int digits) {
    if(digits == 1) {
        return 0;
    }
    return (int) std::pow(10, digits - 1);
}

// 得到在m位数字中，第n位到是什么
int digit_at_n(int n, int digits) {
    // 例如370 = 100 + 881 / 3
    int number = begin_num(digits) + n / digits;
    // 例如1 = 3 - 881 % 3
    // from right 是为了之后求数的时候直接从底位开始
    int n_from_right = digits - n % digits;
    for(int i = 1; i < n_from_right; i++) {
        number /= 10;
    }
    return number % 10;
}

int digit_at_n(int n) {
    if(n < 0) {
        return -1;
    }

    int digits = 1;
    while(true) {
        int numbers = count_of_integers(digits);
        if(n < numbers * digits) {
            return digit_at_n(n, digits);
        }
        n -= digits * numbers;
        digits++;
    }
    return -1;
}

int main() {
    printf("%d\n", digit_at_n(0));
    printf("%d\n", digit_at_n(1000));
    printf("%d\n", digit_at_n(1001));
    printf("%d\n", digit_at_n(1002));
    return 0;
}

面试题45：把数组排成最小的数。

输入一个正整数数组，把数组里所有数字拼接起来排成一个数，打印能拼接出的所有数字中最小的一个。例如，输入{3,32,321}，则打印出这3个数字能排成的最小数字321323
。

基础的思路是全排列，然后找出最小的，时间开销一般是O(n!)，优化的思路也不会很复杂，比如就单看两个数nn和mm，他们两个如何拼接可以最小，也就是比较nnmm和mmnn，那么当整个数组都是前一个数在前面的情况下可以让两个数的结果最小，顺序拼接的结果自然也是最小的（即不会出现比这个结果还小的结果），所以最后问题变成利用这种规则去对数组进行排序。

完整实现代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
#include <iostream>
#include <algorithm> // sort
#include <cstring> // strcpy strcmp strcat

bool g_invalid_input = false;

bool check_data(int* data, int len) {
    g_invalid_input = false;
    if(data == nullptr || len <= 0) {
        g_invalid_input = true;
        return false;
    }
    // 校验是否都是正整数
    for(int i = 0; i < len; i++) {
        if(data[i] <= 0) {
            g_invalid_input = true;
            return false;
        }
    }
    return true;
}

const int MAX_INT_LEN = 10;
// 申请两个全局字符数组，避免排序函数中反复申请，浪费时间
char* g_str_comb1 = new char[MAX_INT_LEN * 2 + 1];
char* g_str_comb2 = new char[MAX_INT_LEN * 2 + 1];

bool compare(const char* num1, const char* num2)
{
    strcpy(g_str_comb1, num1);
    strcat(g_str_comb1, num2);
    strcpy(g_str_comb2, num2);
    strcat(g_str_comb2, num1);
    return strcmp(g_str_comb1, g_str_comb2) == -1;
}

void min_concat(int* data, int len) {
    if(!check_data(data, len)) {
        return;
    }
    // 其实还要考虑两个int相连有可能会超过int表示范围
    // 所以转用字符串可能更合适，同时也不会修改原数据的顺序
    char** str_data = new char*[len];
    for(int i = 0; i < len; i++) {
        str_data[i] = new char[MAX_INT_LEN + 1];
        sprintf(str_data[i], "%d", data[i]);
    }
    std::sort(str_data, str_data + len, compare);
    for(int i = 0; i < len; i++) {
        printf("%s", str_data[i]);
        delete[] str_data[i];
    }
    delete[] str_data;
}

int main() {
    int data[] = {3, 32, 321, 8, 44, 1, 143};
    min_concat(data, 7);
}

代码中需要注意的一个地方是，如果直接用数字排序的方式，可能会在比较nnmm和mmnn时，这种拼接结果超出int的表示范围，而导致错误结果，所以可能出现大数的情况，要注意用字符串来替代处理。另外书上的代码在校验输入的时候，漏掉了对数组的是否是正整数的判断，上面代码也补上了，并且书上代码使用的排序方法是qsort，个人建议使用sort，一般情况下更加效率和便利。

书上有细致的讲，如何去证明这样的方法的正确性（比较规则的三个角度，自反性(aa = aa)、对称性(a<b => ab<ba, ba>ab, => b>a)以及传递性(a<b,b<c => ab<ba, bc<cb => ac<ca)，和反证法，假设结果不是最小的，存在一个更小的，然后去推出假设不成立），尤其是当面试官问到的时候，也要能够说出缘由来，这里就不再复述了。

面试题46：把数字翻译成字符串。

给定一个数字，按照如下规则把它翻译成字符串：0翻译成a，1翻译成b，…，11翻译成l，…，25翻译成z。一个数字可能有多个翻译。例如12258有5种不同的翻译，分别是bccfi、bwf1、bczi、mcfi和mzi。实现一个函数，用来计算一个数字有多少种不同的翻译方法。

直观的递归方法是，12258可以拆解为求解2258和258两个子问题，其中有可分支的条件是c1==1 || (c1==2 && c2 <= 5)，否则只能单线往下求解。

单纯递归完整代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include <iostream>

const int MAX_INT_LEN = 10;

int kinds_of_encode(const char* str_num) {
    if(*str_num == '\0') {
        return 1;
    }
    char c1 = *str_num, c2 = *(str_num + 1);
    if(c1 == '1' || (c1 == '2' && c2 <= '5')) {
        return kinds_of_encode(str_num + 1) + kinds_of_encode(str_num + 2);
    } else {
        return kinds_of_encode(str_num + 1);
    }
}

int kinds_of_encode(int num) {
    if(num < 0) {
        return 0;
    }
    // 用字符数组来处理更加方便一点
    char* str_num = new char[MAX_INT_LEN + 1];
    sprintf(str_num, "%d", num);
    int result = kinds_of_encode(str_num);
    delete[] str_num;
    return result;
}

int main() {
    printf("%d\n", kinds_of_encode(12258)); // 5
    return 0;
}

尽管看起来很简洁，但是这并不是最优的代码，例如2258和258两个子问题，2258会继续分支出258和58，在这一步258子问题被反复求解了，导致了计算的浪费。递归是从最大的问题开始自上而下的解决，其实我们也可以从最小的子问题开始自下而上的解决，来消除重复子问题。

也就是说，从数字的末尾开始，从右到左翻译，并计算不同翻译的数目。

完整实现代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include <iostream>
#include <cstring>

int kinds_of_encode(int num) {
    if(num < 0) {
        return 0;
    }
    // 从右向左翻译，避免重复子问题
    char* str_num = new char[MAX_INT_LEN + 1];
    sprintf(str_num, "%d", num);
    int len = strlen(str_num);
    int* results = new int[len];
    results[len - 1] = 1;
    char c1, c2;
    for(int i = len - 2; i >= 0; i--) {
        c1 = *(str_num + i);
        c2 = *(str_num + i + 1);
        if(c1 == '1' || (c1 == '2' && c2 <= '5')) {
            results[i] = results[i + 1] + results[i + 2];
        } else {
            results[i] = results[i + 1];
        }
    }
    int result = results[0];
    delete[] str_num;
    delete[] results;
    return result;
}

int main() {
    printf("%d\n", kinds_of_encode(12258)); // 5
    return 0;
}

面试题47：礼物的最大价值。

在一个m x n的棋盘的每一格都放有一个礼物，每个礼物都有一定的价值（价值大于0）。可以从棋盘的左上角开始拿格子里的礼物，并每次向右或向下移动一格，直到到达棋盘的右下角。给定一个棋盘以及礼物价值，请问最多能拿到多少价值的礼物？

例如，下面的棋盘中，如果沿着带下划线的数字线路（1、12、5、7、7、16、5），那么我们能拿到最大价值为53的礼物。

定义f(i,j)为到达坐标(i,j)的格子时，能拿到的礼物总和的最大值，我们有两种途径来到达坐标为(i,j)的格子，通过格子(i-1,j)左侧或者(i,j-1)上侧，所以f(i,j)=max(f(i-1,j), f(i,j-1)) + gift[i,j]，gift[i,j]表示坐标(i,j)的格子里礼物的价值。

典型的动态规划问题，定义一个辅助二维数组，数组中(i,j)表示到达该格子时，能拿到的礼物价值总和的最大值。

完整实现代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include <iostream>
#include <algorithm>

int max_gift_value(int** values, int rows, int cols) {
    if(values == nullptr || *values == nullptr || rows <= 0 || cols <= 0) {
        return 0;
    }
    int** max_values = new int*[rows];
    for(int i = 0; i < rows; i++) {
        max_values[i] = new int[cols];
    }
    for(int i = 0; i < rows; i++) {
        for(int j = 0; j < cols; j++) {
            int left = 0, up = 0;
            if(i > 0) {
                up = max_values[i - 1][j];
            }
            if(j > 0) {
                left = max_values[i][j - 1];
            }
            int value = *((int *)values + cols * i + j);
            max_values[i][j] = std::max(left, up) + value;
        }
    }
    int max_value = max_values[rows-1][cols-1];
    for(int i = 0; i < rows; i++) {
        delete[] max_values[i];
    }
    delete[] max_values;
    return max_value;
}

int main() {
    int rows = 4, cols = 4;
    int values[4][4] = {
        {1, 10, 3, 8},
        {12, 2, 9, 6},
        {5, 7, 4, 11},
        {3, 7, 16, 5}
    };
    printf("Max gift value: %d", max_gift_value((int**)values, rows, cols));
    return 0;
}

考虑进一步的优化（主要是空间上），前面我们提到，到达坐标为(i,j)的格子时，最大价值依赖于(i,j-1)左侧和(i-1,j)上侧两个格子，因为此第i-2行及更上面的所有格子礼物的最大价值实际没有保存的必要。我们可以用一个一维数组来替代前面代码中的二维数组max_values，一维数组的长度为cols。

优化之后的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
int max_gift_value(int** values, int rows, int cols) {
    if(values == nullptr || *values == nullptr || rows <= 0 || cols <= 0) {
        return 0;
    }
    int* max_values = new int[rows]; // 修改为一维数组
    for(int i = 0; i < rows; i++) {
        for(int j = 0; j < cols; j++) {
            int left = 0, up = 0;
            if(i > 0) {
                up = max_values[j]; // 此时j位置保存的为上一行的数据
            }
            if(j > 0) {
                left = max_values[j - 1]; // 此时j-1位置已经是该行的数据
            }
            int value = *((int *)values + cols * i + j);
            max_values[j] = std::max(left, up) + value; // 更新j为该行的数据
        }
    }
    int max_value = max_values[cols-1];
    delete[] max_values;
    return max_value;
}

面试题48：最长不含重复字符的子字符串。

请从字符串中找出一个最长的不包含重复字符的子字符串，计算该最长子字符串的长度。假设字符串中只包含a~z。例如arabcacfr中，最长的不包含重复字符的子字符串是acfr，长度是4(还有子串rabc)。

这道题其实和之前的最大子数组和（面试题42）的思路有异曲同工之妙，同样有两种方法，一种是通过规律观察，另一种就是书上讲的动态规划法。首先讲一下这类“连续子串的最大/小”问题的一种规律解法，申明两个指针从头开始，头指针指向子串的头部，尾指针指向子串的尾部，尾指针每一步都向后移动一尾，同时根据移动后尾指针访问的状况（以及结合之前的值）来判断如何移动头指针。在本题目中，约束条件是不包含重复字符，也就是说当尾指针访问到一个重复字符时，就要调整头指针移向下一个不会让子串出现重复字符的位置（也就是跳到下一个满足约束的子串），记录过程中子串的最大长度，最后返回最大长度，时间复杂度O(n)。

完整实现代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include <iostream>
#include <map>
#include <cstring>

int longest_substr_no_dup(char* str) {
    if(str == nullptr || strlen(str) == 0) {
        return 0;
    }
    std::map<char, bool> char_map;
    // 初始化map
    for(int i = 0; i < 26; i++) {
        char_map['a'+i] = false;
    }
    char* start = str;
    char* end = str;
    int len = 0;
    int max_len = 0;
    for(int i = 0; i < strlen(str); i++) {
        if(!char_map[*end]) {
            // 没有遇到重复字符，子串长度+1
            len++;
            max_len = (max_len < len) ? len : max_len;
            char_map[*end] = true;
            end++;
        } else {
            // 直到start遇到该重复字符为止
            while(*start != *end) {
                char_map[*start] = false;
                start++;
                len--;
            }
            start++;
            char_map[*end] = true;
            end++;
        }
    }
    return max_len;
}

int main() {
    char* str = "arabcacfr";
    printf("%s longest substr no dup: %d", str, longest_substr_no_dup(str));
}

代码中使用到了std::map<char, bool>来记录当前子串的字符出现情况，也可以自行建立一个bool数组实现记录。

然后再看一下书上的动态规划思路（其实和面试题42的动态规划解法也类似），定义f(i)表示以第i个字符结尾的不包含重复字符的子串的最长长度。如果是从左到右的计算顺序，当我们计算f(i)的时候f(i-1)已经被计算出了。

  • 如果第i个字符没有出现过，那么f(i)=f(i-1)+1；
  • 如果第i个字符之前已经出现过了，要先计算第i个字符和它上次出现在字符串中位置的距离，记为d，接着要分两种情况：
    • 如果d <= f(i-1)，此时第i个字符上次出现在f(i-1)对应的最长子字符串之中，因此f(i)=d；
    • 如果d > f(i-1)，此时第i个字符上次出现在f(i-1)对应的最长子字符串之前，因此仍然有f(i)=f(i-1)+1。

完整实现代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
int longest_substr_no_dup(char* str) {
    if(str == nullptr || strlen(str) == 0) {
        return 0;
    }
    int len = 0;
    int max_len = 0;
    int str_len = strlen(str);
    int* position = new int[26]; // 存储每个字符上次出现的下标
    for(int i = 0; i < 26; i++) {
        position[i] = -1;
    }
    for(int i = 0; i < str_len; i++) {
        int prev_index = position[*(str+i) - 'a'];
        if(prev_index < 0 || i - prev_index > len) {
            len++;
        } else {
            if(len > max_len) {
                max_len = len;
            }
            len = i - prev_index;
        }
        position[*(str+i) - 'a'] = i;
    }
    if(len > max_len) {
        max_len = len;
    }
    delete position;
    return max_len;
}

3 时间与空间的平衡

由于内存的容量增加迅速，在软件开发的过程中我们允许以牺牲一定的空间为代价来优化时间性能，以尽可能地缩短软件的响应时间。这就是我们通常所说的“以空间换时间”。

在面试的时候，如果我们分配少量的辅助空间来保存计算的中间结果以提高时间效率，则通常是可以被接受的。

但“空间换时间”并不一定都是可行的，面试的时候要具体问题具体分析，也就是对时间和空间的平衡考量。

面试题 49-52

面试题49：丑数。

把只包含因子2、3和5的数称作丑数(Ugly Number）。求按从小到大的顺序的第1500个丑数。例如6、8都是丑数，但14不是。习惯上把1当作第1个丑数。

判断一个数是不是丑数的方法，就是依次除以因数2、3、5，每一个因数都是无法再除了再除下一个因数，如果三个因数都除尽了，剩下的为1，则为丑数，否则不是丑数，简单实现的判别函数：

1
2
3
4
5
6
7
8
9
10
11
12
bool is_ugly(int number) {
    while(number % 2 == 0) {
        number /= 2;
    }
    while(number % 3 == 0) {
        number /= 3;
    }
    while(number % 5 == 0) {
        number /= 5;
    }
    return (number == 1) ? true : false;
}

每个数依次的判别是不是丑数肯定是不够高效的。

优化思路：创建数组保存已找到的丑数，用空间换时间的解法。

根据丑数的定义，丑数应该是另一个丑数乘以2、3或者5的结果（1除外），因此，我们可以创建一个数组，里面数字是排好序的丑数，每个丑数都是前面的丑数乘以2、3或者5得到的。

这种思路的关键在于怎么确保数组里面的丑数排好序。假设数组已有若干个排好序的丑数，把最大的丑数记为M，分析如何生成下一个丑数。下一个丑数肯定是前面某一个丑数乘以2、3或者5得到的，并且我们仅仅需要第一个大于M的丑数，也不用去乘以前方的所有丑数，其中一定有一个丑数满足一个条件，他是从小到大的第一个乘以2会大于M的丑数，记为T_2，类似的有T_3、T_5，每一次我们只需要在T_2 * 2和T_3 * 3和T_5 * 5中找到较小的一个即可（并且要更新所有T）。

完整实现代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include <iostream>

int min(int num1, int num2, int num3) {
    int min = (num1 < num2) ? num1 : num2;
    min = (min < num3) ? min : num3;
    return min;
}

int ugly_num_at_n(int n) {
    if(n <= 0) {
        return 0;
    }
    int *ugly_nums = new int[n];
    ugly_nums[0] = 1;
    int next_ugly_index = 1;

    int* pt2 = ugly_nums;
    int* pt3 = ugly_nums;
    int* pt5 = ugly_nums;

    while(next_ugly_index < n) {
        int min_num = min(*pt2 * 2, *pt3 * 3, *pt5 * 5);
        ugly_nums[next_ugly_index] = min_num;
        while(*pt2 * 2 <= min_num) {
            pt2++;
        }
        while(*pt3 * 3 <= min_num) {
            pt3++;
        }
        while(*pt5 * 5 <= min_num) {
            pt5++;
        }
        next_ugly_index++;
    }
    int ugly = ugly_nums[n - 1];
    delete[] ugly_nums;
    return ugly;
}

int main() {
    printf("Ugly Num at %d is %d\n", 1500, ugly_num_at_n(1500)); // 859963392
    printf("Ugly Num at %d is %d\n", 5, ugly_num_at_n(5)); // 5
    printf("Ugly Num at %d is %d\n", 1, ugly_num_at_n(1)); // 1
}

面试题50：第一次只出现一次的字符。

题目一：字符串中第一个只出现一次的字符。

在字符串中找出第一个只出现一次的字符。如输入abaccdeff，则输出b。

直接的思路是每次都比较一个字符是否在其后面出现，这种思路的时间复杂度是O(n^2)，效率不够高，可以考虑用空间换时间。如果我们可以统计每个字符出现的次数，可能就会变得简单的多，一般也用哈希表来解决这种问题。

哈希表是一种比较复杂的数据结构，C++标准模板库中的map和unordered_map实现了哈希表的功能，可以直接用。由于本题的特殊性，我们其实只需要一个非常简单的哈希表就能满足要求，因此我们可以考虑实现一个简单的哈希表。字符(char)是一个长度为8(bit)的数据类型，因此总共有256种可能性。我们创建一个长度为256的数组，每个字母根据其ASCII码值作为数组的下标对应数组的一个数组，而数组中存储的是每个字符出现的次数。这样我们就创建了一个大小为256、以字符ASCII码为键值的哈希表。

第一次扫描时，更新一个字符的出现次数需要时间O(1)，总共O(n)；第二次扫描时，寻找第一个出现次数为1的字符，时间也是O(n)。同时我们需要一个辅助数组，大小是1KB，由于数组大小是一个常数，因此认为这种算法的空间复杂度是O(1)。

完整实现代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include <iostream>

char first_unique_char(char* str) {
    if(str == nullptr) {
        return '\0';
    }
    const int TABLE_SIZE = 256;
    unsigned int hash_table[TABLE_SIZE];
    for(unsigned int i = 0; i < TABLE_SIZE; i++) {
        hash_table[i] = 0;
    }
    char* pchar = str;
    while(*pchar != '\0') {
        hash_table[*pchar]++;
        pchar++;
    }
    pchar = str;
    while(*pchar != '\0') {
        if(hash_table[*pchar] == 1) {
            return *pchar;
        }
        pchar++;
    }
    return '\0';
}

int main() {
    char* str = "abaccdeff";
    printf("First unique char of %s is %c", str, first_unique_char(str));
    return 0;
}

题目二：字符流中第一个只出现一次的字符。

实现一个函数，用来找出字符流中第一个只出现一次的字符。例如，字符流只读出go时，第一个只出现一次的字符是g；当读出google时，第一个只出现一次的字符时l。

可以定义一个数据容器来保存字符在字符流中的位置。当一个字符第一次从字符流读出来时，把位置保存在数据容器中。当字符再次从字符流中读取时，这时把它在容器中保存的值更新为一个特殊值（如负数）。而在查找第一个只出现一次的字符时，只需要遍历容器，找到最小的位置即可。

完整实现代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
#include <iostream>
#include <limits.h>

class CharStatistics {
    public:
        CharStatistics(): index(0) {
            for(int i = 0; i < 256; i++) {
                occurrence[i] = -1;
            }
        }

        void insert(char ch) {
            if(occurrence[ch] == -1) {
                occurrence[ch] = index;
            } else if(occurrence[ch] >= 0) {
                occurrence[ch] = -2;
            }
            index++;
        }

        char first_unique_char() {
            char ch = '\0';
            int min_index = INT_MAX;
            for(int i = 0; i < 256; i++) {
                if(occurrence[i] >= 0 && occurrence[i] < min_index) {
                    ch = (char)i;
                    min_index = occurrence[i];
                }
            }
            return ch;
        }

    private:
        // occurrence[i] : A char with ASCII value i;
        // occurrence[i] = -1 : not found yet
        // occurrence[i] = -2 : have been found for mutlple times
        // occurrence[i] >= 0 : have been found only once
        int occurrence[256];
        int index;
};

int main() {
    CharStatistics char_statistics;
    char* stream = "google";
    for(int i = 0; i < 6; i++) {
        char_statistics.insert(stream[i]);
        printf("After insert %c, first unique char is %c\n", stream[i],
            char_statistics.first_unique_char());
    }
    return 0;
}

面试题51：数组中的逆序对。

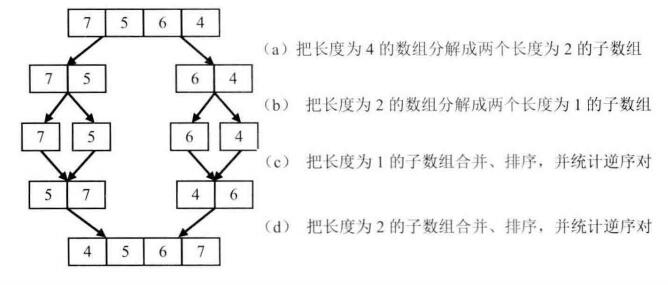
在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组，求出这个数组中的逆序对的总数。例如，数组{7,5,6,4}中，一共有5个逆序对，分别是(7,5)、(7,6)、(7,4)、(5,4)和(6,4)。

统计逆序对的过程

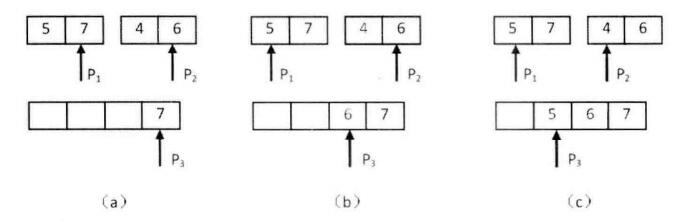
(d)中合并两个子数组并统计逆序对的过程

  • (a) P1指向的数字大于P2指向的数字（先比较最大的），表示数组中存在逆序对，把逆序对数目加2（后一个子数组的长度），并把7复制到辅助数组，向前移动P1和P3；
  • (b) P1指向的数字小于P2指向的数字，没有逆序对。把P2指向的数字复制到辅助数组，并向前移动P2和P3；
  • (c) P1指向的数字大于P2指向的数字，存在逆序对，把逆序对数目加1（后一个子数组的剩余长度），把5复制到辅助数组，想前移动P1和P3；
  • (…) 直到只剩一个元素，复制到辅助数组，结束合并，开始下一次相邻数组的合并。

过程有点类似与归并排序，不过为了统计逆序对，从尾部开始合并。

完整实现代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
#include <iostream>

int inverse_pair_core(int* data, int* copy, int start, int end) {
    if(start == end) {
        copy[start] == data[start];
        return 0;
    }
    int len = (end - start) / 2;
    // 注意这里交换了copy和data的位置，实现了交替使用
    // 一次合并排序的结果保存在data中
    int left = inverse_pair_core(copy, data, start, start + len);
    int right = inverse_pair_core(copy, data, start + len + 1, end);

    int i = start + len;
    int j = end;
    int index_copy = end;
    int count = 0;

    while(i >= start && j >= start + len + 1) {
        if(data[i] > data[j]) {
            // 前面的大于后面的
            copy[index_copy--] = data[i--];
            count += j - start - len;
        } else {
            // 前面的小于后面的
            copy[index_copy--] = data[j--];
        }
    }
    // 拷贝剩余的
    while(i >= start) {
        copy[index_copy--] = data[i--];
    }
    while(j >= start + len + 1) {
        copy[index_copy--] = data[j--];
    }
    return left + right + count;
}

int inverse_pair(int* data, int len) {
    if(data == nullptr || len <= 0) {
        return 0;
    }

    int* copy = new int[len];
    for(int i = 0; i < len; i++) {
        copy[i] = data[i];
    }
    int count = inverse_pair_core(data, copy, 0, len - 1);
    delete[] copy;
    return count;
}

int main() {
    int data[] = {7,5,6,4};
    printf("Data have %d inverse pair.\n", inverse_pair(data, 4));
    return 0;
}

归并排序的时间复杂度是O(nlogn)，比直观方法的O(n^2)要快，但同时归并需要一个长度为n的辅助数组，所以用了O(n)的空间来换时间效率的提升。

面试题52：两个链表的第一个公共节点。

输入两个链表，找出他们的第一个公共节点。链表节点定义如下：

1
2
3
4
struct node {
    int key;
    node* pnext;
}

其实有之前题目的铺垫，这里蛮容易想到根据两个链不同长度来调整起始指针的位置，调整起始后的两个指针，同步移动，当相遇时就是两个链表的公共节点，时间复杂度O(m+n)，m和n是两个链表的长度。

完整实现代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
#include <iostream>

struct node {
    int key;
    node* pnext;
};

node* init_node(int key) { ... }
void init_list(node** pphead1, node** pphead2) { ... }

int get_list_len(node* phead) {
    unsigned int len = 0;
    node* pnode = phead;
    while(pnode != nullptr) {
        len++;
        pnode = pnode->pnext;
    }
    return len;
}

node* find_first_common_node(node* phead1, node* phead2) {
    unsigned int len1 = get_list_len(phead1);
    unsigned int len2 = get_list_len(phead2);
    if(len1 == 0 || len2 == 0) {
        return nullptr;
    }

    int len_diff = len1 - len2;
    node* plong_list = phead1;
    node* pshort_list = phead2;
    if(len2 > len1) {
        len_diff = len2 - len1;
        plong_list = phead2;
        pshort_list = phead1;
    }

    for(int i = 0; i < len_diff; i++) {
        plong_list = plong_list->pnext;
    }

    while(plong_list != nullptr && pshort_list != nullptr
          && plong_list != pshort_list) {
        plong_list = plong_list->pnext;
        pshort_list = pshort_list->pnext;
    }

    return plong_list;
}

int main() {
    node* phead1;
    node* phead2;
    init_list(&phead1, &phead2);
    node* first_common_node = find_first_common_node(phead1, phead2);
    printf("First common node is %d\n", first_common_node->key);
    return 0;
}

书上还提到了一种方法，非常的巧妙，尤其是在这种需要在单向链表反向查找时，可以使用一个栈来实现逆向查询，例如在本题中，如果我们可以从两个链表的尾节点开始逆向查找，那么最后一个相同的节点，也就是第一个公共节点，可以使用两个栈来实现这个过程，时间开销O(m+n)，空间开销O(m+n)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
node* find_first_common_node(node* phead1, node* phead2) {
    if(phead1 == nullptr || phead2 == nullptr) {
        return nullptr;
    }
    std::vector<node*> stk1, stk2;
    while(phead1 != nullptr) {
        stk1.push_back(phead1);
        phead1 = phead1->pnext;
    }
    while(phead2 != nullptr) {
        stk2.push_back(phead2);
        phead2 = phead2->pnext;
    }
    node* common_node = nullptr;
    while(!stk1.empty() && !stk2.empty()) {
        if(stk1[stk1.size() - 1] == stk2[stk2.size() - 1]) {
            common_node = stk1[stk1.size() - 1];
        }
        stk1.pop_back();
        stk2.pop_back();
    }
    return common_node;
}

后一种方法虽然多了一个O(m+n)的空间开销，但是在一些单纯链表方法不能方便解决的时候，也不妨是一种构思的思路。

4 总结

编程面试时，面试官通常对时间复杂度和空间复杂度都会有要求，并且一般情况下面试官更加关注时间复杂度。

降低时间复杂度的第一种方法是改用更加高效的算法；第二种方法是用空间换时间。

以空间换时间并不一定都是可行的方案，还要注意辅助空间的大小，消耗空间过大也是得不偿失的。

《剑指Offer》第5章笔记 优化效率

https://yumi-cn.github.io/2021/01/11/s2o-c5-optimize/

作者

Yumiko

发布于

2021-01-11

更新于

2021-01-14

许可协议

#

喜欢这篇文章？打赏一下作者吧

评论

关注我

专栏

最新文章

×