《LearnOpenGL》入门 笔记
Hello OpenGL!
笔记摘录源地址:LearnOpenGL CN
OpenGL
创建窗口
你好,窗口
1 |
|
你好,三角形
- 顶点数组对象:Vertex Array Object,VAO
- 顶点缓冲对象:Vertex Buffer Object,VBO
- 索引缓冲对象:Element Buffer Object,EBO或Index Buffer Object,IBO
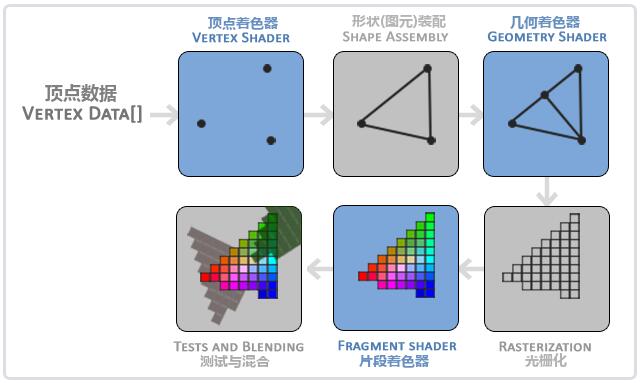
3D坐标转为2D坐标的处理过程是由OpenGL的图形渲染管线(Graphics Pipeline,大多译为管线,实际上指的是一堆原始图形数据途经一个输送管道,期间经过各种变化处理最终出现在屏幕的过程)管理的。
图形渲染管线可以被划分为两个主要部分:
- 第一部分把你的3D坐标转换为2D坐标;
- 第二部分是把2D坐标转变为实际的有颜色的像素。
2D坐标和像素也是不同的,2D坐标精确表示(通常是浮点数的形式)一个点在2D空间中的位置,而2D像素是这个点的近似值,2D像素受到你的屏幕/窗口分辨率的限制。
图形渲染管线可以被划分为几个阶段,每个阶段将会把前一个阶段的输出作为输入。所有这些阶段都是高度专门化的(它们都有一个特定的函数),并且很容易并行执行。正是由于它们具有并行执行的特性,当今大多数显卡都有成千上万的小处理核心,它们在GPU上为每一个(渲染管线)阶段运行各自的小程序,从而在图形渲染管线中快速处理你的数据。这些小程序叫做着色器(Shader)。
有些着色器允许开发者自己配置,这就允许我们用自己写的着色器来替换默认的。这样我们就可以更细致地控制图形渲染管线中的特定部分了,而且因为它们运行在GPU上,所以它们可以给我们节约宝贵的CPU时间。OpenGL着色器是用OpenGL着色器语言(OpenGL Shading Language, GLSL)写成的,在下一节中我们再花更多时间研究它。
首先,我们以数组的形式传递3个3D坐标作为图形渲染管线的输入,用来表示一个三角形,这个数组叫做顶点数据(Vertex Data);顶点数据是一系列顶点的集合。一个顶点(Vertex)是一个3D坐标的数据的集合。而顶点数据是用顶点属性(Vertex Attribute)表示的,它可以包含任何我们想用的数据。
为了让OpenGL知道我们的坐标和颜色值构成的到底是什么,OpenGL需要你去指定这些数据所表示的渲染类型。是希望把这些数据渲染成一系列的点?一系列的三角形?还是仅仅是一个长长的线?做出的这些提示叫做图元(Primitive),任何一个绘制指令的调用都将把图元传递给OpenGL。这是其中的几个:GL_POINTS、GL_TRIANGLES、GL_LINE_STRIP。
图形渲染管线的第一个部分是顶点着色器(Vertex Shader),它把一个单独的顶点作为输入。顶点着色器主要的目的是把3D坐标转为另一种3D坐标(后面会解释),同时顶点着色器允许我们对顶点属性进行一些基本处理。
图元装配(Primitive Assembly)阶段将顶点着色器输出的所有顶点作为输入(如果是GL_POINTS,那么就是一个顶点),并所有的点装配成指定图元的形状。
图元装配阶段的输出会传递给几何着色器(Geometry Shader)。几何着色器把图元形式的一系列顶点的集合作为输入,它可以通过产生新顶点构造出新的(或是其它的)图元来生成其他形状。
几何着色器的输出会被传入光栅化阶段(Rasterization Stage),这里它会把图元映射为最终屏幕上相应的像素,生成供片段着色器(Fragment Shader)使用的片段(Fragment)。在片段着色器运行之前会执行裁切(Clipping)。裁切会丢弃超出你的视图以外的所有像素,用来提升执行效率。
OpenGL中的一个片段(Fragment)是OpenGL渲染一个像素所需的所有数据。
片段着色器(Fragment Shader or Pixel Shader)的主要目的是计算一个像素的最终颜色,这也是所有OpenGL高级效果产生的地方。通常,片段着色器包含3D场景的数据(比如光照、阴影、光的颜色等等),这些数据可以被用来计算最终像素的颜色。
在所有对应颜色值确定以后,最终的对象将会被传到最后一个阶段,我们叫做Alpha测试和混合(Blending)阶段。这个阶段检测片段的对应的深度(和模板(Stencil))值(后面会讲),用它们来判断这个像素是其它物体的前面还是后面,决定是否应该丢弃。这个阶段也会检查alpha值(alpha值定义了一个物体的透明度)并对物体进行混合(Blend)。所以,即使在片段着色器中计算出来了一个像素输出的颜色,在渲染多个三角形的时候最后的像素颜色也可能完全不同。
可以看到,图形渲染管线非常复杂,它包含很多可配置的部分。然而,对于大多数场合,我们只需要配置顶点和片段着色器就行了,几何着色器是可选的,通常使用它默认的着色器就行了。
在现代OpenGL中,我们必须定义至少一个顶点着色器和一个片段着色器(因为GPU中没有默认的顶点/片段着色器)。出于这个原因,刚开始学习现代OpenGL的时候可能会非常困难,因为在你能够渲染自己的第一个三角形之前已经需要了解一大堆知识了。
顶点输入
开始绘制图形之前,我们必须先给OpenGL输入一些顶点数据。OpenGL是一个3D图形库,所以我们在OpenGL中指定的所有坐标都是3D坐标(x、y和z)。OpenGL仅当3D坐标在3个轴(x、y和z)上都为-1.0到1.0的范围内时才处理它。所有在所谓的标准化设备坐标(Normalized Device Coordinates)范围内的坐标才会最终呈现在屏幕上(在这个范围以外的坐标都不会显示)。
由于我们希望渲染一个三角形,我们一共要指定三个顶点,每个顶点都有一个3D位置。我们会将它们以标准化设备坐标的形式(OpenGL的可见区域)定义为一个float数组。
1 | float vertices[] = { |
由于OpenGL是在3D空间中工作的,而我们渲染的是一个2D三角形,我们将它顶点的z坐标设置为0.0。这样子的话三角形每一点的深度(Depth)都是一样的,从而使它看上去像是2D的。
标准化设备坐标(Normalized Device Coordinates, NDC):一旦你的顶点坐标已经在顶点着色器中处理过,它们就应该是标准化设备坐标了,标准化设备坐标是一个x、y和z值在-1.0到1.0的一小段空间。任何落在范围外的坐标都会被丢弃/裁剪,不会显示在你的屏幕上。下面你会看到我们定义的在标准化设备坐标中的三角形(忽略z轴):
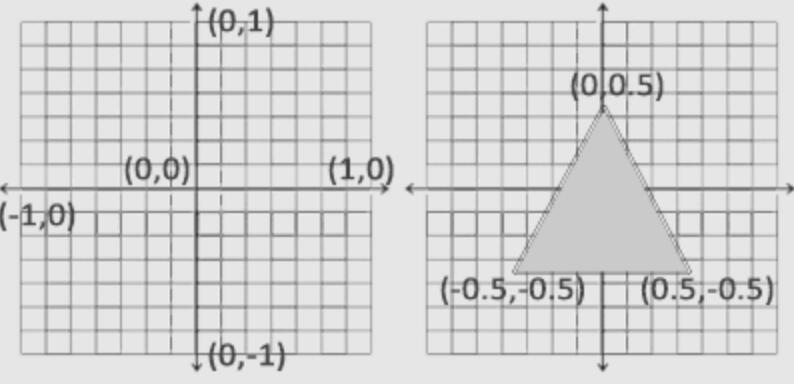
与通常的屏幕坐标不同,y轴正方向为向上,(0, 0)坐标是这个图像的中心,而不是左上角。最终你希望所有(变换过的)坐标都在这个坐标空间中,否则它们就不可见了。
你的标准化设备坐标接着会变换为屏幕空间坐标(Screen-space Coordinates),这是使用你通过glViewport函数提供的数据,进行视口变换(Viewport Transform)完成的。所得的屏幕空间坐标又会被变换为片段输入到片段着色器中。
定义这样的顶点数据以后,我们会把它作为输入发送给图形渲染管线的第一个处理阶段:顶点着色器。它会在GPU上创建内存用于储存我们的顶点数据,还要配置OpenGL如何解释这些内存,并且指定其如何发送给显卡。顶点着色器接着会处理我们在内存中指定数量的顶点。
我们通过顶点缓冲对象(Vertex Buffer Objects, VBO)管理这个内存,它会在GPU内存(通常被称为显存)中储存大量顶点。使用这些缓冲对象的好处是我们可以一次性的发送一大批数据到显卡上,而不是每个顶点发送一次。从CPU把数据发送到显卡相对较慢,所以只要可能我们都要尝试尽量一次性发送尽可能多的数据。当数据发送至显卡的内存中后,顶点着色器几乎能立即访问顶点,这是个非常快的过程。
顶点缓冲对象是我们在OpenGL教程中第一个出现的OpenGL对象。就像OpenGL中的其它对象一样,这个缓冲有一个独一无二的ID,所以我们可以使用glGenBuffers函数和一个缓冲ID生成一个VBO对象:
1 | unsigned int VBO; |
OpenGL有很多缓冲对象类型,顶点缓冲对象的缓冲类型是GL_ARRAY_BUFFER。OpenGL允许我们同时绑定多个缓冲,只要它们是不同的缓冲类型。我们可以使用glBindBuffer函数把新创建的缓冲绑定到GL_ARRAY_BUFFER目标上:
1 | glBindBuffer(GL_ARRAY_BUFFER, VBO); |
从这一刻起,我们使用的任何(在GL_ARRAY_BUFFER目标上的)缓冲调用都会用来配置当前绑定的缓冲(VBO)。然后我们可以调用glBufferData函数,它会把之前定义的顶点数据复制到缓冲的内存中:
1 | glBufferData(GL_ARRAY_BUFFER, sizeof(vertices), vertices, GL_STATIC_DRAW); |
glBufferData是一个专门用来把用户定义的数据复制到当前绑定缓冲的函数。
- 第一个参数是目标缓冲的类型:顶点缓冲对象当前绑定到GL_ARRAY_BUFFER目标上;
- 第二个参数指定传输数据的大小(以字节为单位);用一个简单的sizeof计算出顶点数据大小就行;
- 第三个参数是我们希望发送的实际数据;
- 第四个参数指定了我们希望显卡如何管理给定的数据。它有三种形式:
- GL_STATIC_DRAW:数据不会或几乎不会改变;
- GL_DYNAMIC_DRAW:数据会被改变很多;
- GL_STREAM_DRAW:数据每次绘制时都会改变。
- 三角形的位置数据不会改变,每次渲染调用时都保持原样,所以它的使用类型最好是GL_STATIC_DRAW;
- 如果,比如说一个缓冲中的数据将频繁被改变,那么使用的类型就是GL_DYNAMIC_DRAW或GL_STREAM_DRAW,这样就能确保显卡把数据放在能够高速写入的内存部分。
现在我们已经把顶点数据储存在显卡的内存中,用VBO这个顶点缓冲对象管理。下面我们会创建一个顶点和片段着色器来真正处理这些数据。
顶点着色器 Vertex Shader
我们需要做的第一件事是用着色器语言GLSL(OpenGL Shading Language)编写顶点着色器,然后编译这个着色器,这样我们就可以在程序中使用它了。下面你会看到一个非常基础的GLSL顶点着色器的源代码:
1 |
|
GLSL看起来很像C语言。每个着色器都起始于一个版本声明。OpenGL 3.3以及和更高版本中,GLSL版本号和OpenGL的版本是匹配的(比如说GLSL 420版本对应于OpenGL 4.2)。我们同样明确表示我们会使用核心模式。
下一步,使用in关键字,在顶点着色器中声明所有的输入顶点属性(Input Vertex Attribute)。现在我们只关心位置(Position)数据,所以我们只需要一个顶点属性。GLSL有一个向量数据类型,它包含1到4个float分量,包含的数量可以从它的后缀数字看出来。由于每个顶点都有一个3D坐标,我们就创建一个vec3输入变量aPos。我们同样也通过layout (location = 0)设定了输入变量的位置值(Location)你后面会看到为什么我们会需要这个位置值。
向量(Vector):在GLSL中一个向量有最多4个分量,每个分量值都代表空间中的一个坐标,它们可以通过vec.x、vec.y、vec.z和vec.w来获取。注意vec.w分量不是用作表达空间中的位置的(我们处理的是3D不是4D),而是用在所谓透视除法(Perspective Division)上。
为了设置顶点着色器的输出,我们必须把位置数据赋值给预定义的gl_Position变量,它在幕后是vec4类型的。在main函数的最后,gl_Position设置的值会成为该顶点着色器的输出。
当前这个顶点着色器可能是我们能想到的最简单的顶点着色器了,因为我们对输入数据什么都没有处理就把它传到着色器的输出了。在真实的程序里输入数据通常都不是标准化设备坐标,所以我们首先必须先把它们转换至OpenGL的可视区域内。
编译着色器
上面写的顶点着色器源码存储在一个C字符串中,为了能让OpenGL能使用它,我们必须在运行时动态编译它的源码。
我们首先要做的是创建一个着色器对象,注意还是用ID来引用的。所以我们储存这个顶点着色器为unsigned int,然后用glCreateShader创建这个着色器:
1 | unsigned int vertexShader; |
我们把需要创建的着色器类型以参数形式提供给glCreateShader。由于我们正在创建一个顶点着色器,传递的参数是GL_VERTEX_SHADER。
下一步我们把这个着色器源码附加到着色器对象上,然后编译它:
1 | glShaderSource(vertexShader, 1, &vertexShaderSource, NULL); |
glShaderSource函数:
- 把要编译的着色器对象作为第一个参数;
- 第二参数指定了传递的源码字符串数量,这里只有一个;
- 第三个参数是顶点着色器真正的源码;
- 第四个参数我们先设置为NULL。
检测编译时错误可以通过以下代码来实现:
1 | int success; |
首先我们定义一个整型变量来表示是否成功编译,还定义了一个储存错误消息(如果有的话)的容器。然后我们用glGetShaderiv检查是否编译成功。如果编译失败,我们会用glGetShaderInfoLog获取错误消息,然后打印它。
1 | if(!success) { |
如果编译的时候没有检测到任何错误,顶点着色器就被编译成功了。
片段着色器
片段着色器(Fragment Shader)是第二个也是最后一个我们打算创建的,用于渲染三角形的着色器。段着色器所做的是计算像素最后的颜色输出。为了让事情更简单,我们的片段着色器将会一直输出橘黄色(1.0f, 0.5f, 0.2f)。
在计算机图形中颜色被表示为有4个元素的数组:红色(R)、绿色(G)、蓝色(B)和alpha(透明度)分量(A),通常缩写为RGBA。当在OpenGL或GLSL中定义一个颜色的时候,我们把颜色每个分量的强度设置在0.0到1.0之间。比如说我们设置红为1.0f,绿为1.0f,我们会得到两个颜色的混合色,即黄色。这三种颜色分量的不同调配可以生成超过1600万种不同的颜色!
1 |
|
片段着色器只需要一个输出变量,这个变量是一个4分量向量,它表示的是最终的输出颜色,我们应该自己将其计算出来。我们可以用out关键字声明输出变量,这里我们命名为FragColor。下面,我们将一个alpha值为1.0(1.0代表完全不透明)的橘黄色的vec4赋值给颜色输出。
编译片段着色器的过程与顶点着色器类似,只不过我们使用GL_FRAGMENT_SHADER常量作为着色器类型:
1 | unsigned int fragmentShader; |
两个着色器现在都编译了,剩下的事情是把两个着色器对象链接到一个用来渲染的着色器程序(Shader Program)中。
着色器程序
着色器程序对象(Shader Program Object)是多个着色器合并之后并最终链接完成的版本。如果要使用刚才编译的着色器(顶点、片段),我们必须把它们链接(Link)为一个着色器程序对象,然后在渲染对象的时候激活这个着色器程序。已激活着色器程序的着色器将在我们发送渲染调用(draw call)的时候被使用。
当链接着色器至一个程序的时候,它会把每个着色器的输出链接到下个着色器的输入。当输出和输入不匹配的时候,你会得到一个连接错误。
创建一个程序对象:
1 | unsigned int shaderProgram; |
glCreateProgram函数创建一个程序,并返回新创建程序对象的ID引用。现在我们需要把之前编译的着色器附加(glAttachShader)到程序对象上,然后用glLinkProgram链接它们:
1 | glAttachShader(shaderProgram, vertexShader); |
代码应该很清楚,我们把着色器附加到了程序上,然后用glLinkProgram链接。
就像着色器的编译一样,我们也可以检测链接着色器程序是否失败,并获取相应的日志。与上面不同,我们不会调用glGetShaderiv和glGetShaderInfoLog,现在我们使用:
1 | int success; |
得到的结果就是一个程序对象,我们可以调用glUseProgram函数,用刚创建的程序对象作为它的参数,以激活这个程序对象:
1 | glUseProgram(shaderProgram); |
在glUseProgram函数调用之后,每个着色器调用和渲染调用都会使用这个程序对象(也就是之前写的着色器)了。
对了,在把着色器对象链接到程序对象以后,记得删除着色器对象,我们不再需要它们了:
1 | glDeleteShader(vertexShader); |
现在,我们已经把输入顶点数据发送给了GPU,并指示了GPU如何在顶点和片段着色器中处理它。就快要完成了,但还没结束,OpenGL还不知道它该如何解释内存中的顶点数据,以及它该如何将顶点数据链接到顶点着色器的属性上。我们需要告诉OpenGL怎么做。
链接顶点属性
顶点着色器允许我们指定任何以顶点属性为形式的输入。这使其具有很强的灵活性的同时,它还的确意味着我们必须手动指定输入数据的哪一个部分对应顶点着色器的哪一个顶点属性。所以,我们必须在渲染前指定OpenGL该如何解释顶点数据。
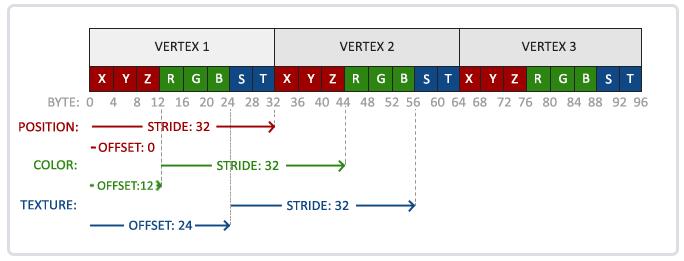
顶点缓冲数据会被解析为下面这样子:
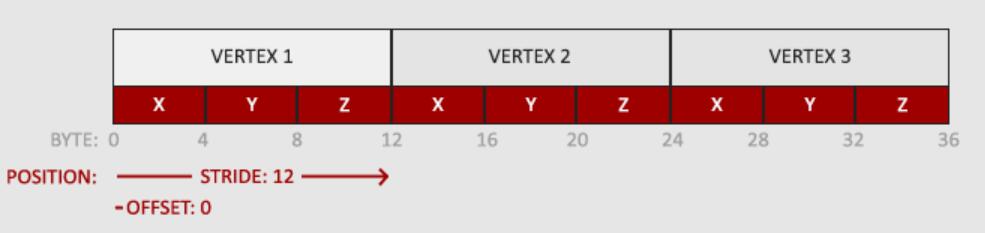
- 位置数据被储存为32位(4字节)浮点值;
- 每个位置包含3个这样的值;
- 这几个值在数组中紧密排列(Tightly Packed);
- 数据中第一个值在缓冲开始的位置。
有了这些信息我们就可以使用glVertexAttribPointer函数告诉OpenGL该如何解析顶点数据(应用到逐个顶点属性上)了:
1 | glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, 3 * sizeof(float), (void*)0); |
glVertexAttribPointer函数的参数非常多,所以我会逐一介绍它们:
- 第一个参数指定我们要配置的顶点属性。还记得我们在顶点着色器中使用
layout(location = 0)定义了position顶点属性的位置值(Location)吗?它可以把顶点属性的位置值设置为0。因为我们希望把数据传递到这一个顶点属性中,所以这里我们传入0; - 第二个参数指定顶点属性的大小。顶点属性是一个vec3,它由
3个值组成,所以大小是3; - 第三个参数指定数据的类型,这里是GL_FLOAT(GLSL中vec*都是由浮点数值组成的)。
- 第四个参数定义我们是否希望数据被标准化(Normalize)。如果我们设置为GL_TRUE,所有数据都会被映射到0(对于有符号型signed数据是-1)到1之间。我们把它设置为GL_FALSE,所有数据不会被处理。
- 第五个参数叫做步长(Stride),它告诉我们在连续的顶点属性组之间的间隔。由于下个组位置数据在3个float之后,我们把步长设置为
3 * sizeof(float)。要注意的是由于我们知道这个数组是紧密排列的(在两个顶点属性之间没有空隙)我们也可以设置为0来让OpenGL决定具体步长是多少(只有当数值是紧密排列时才可用)。一旦我们有更多的顶点属性,我们就必须更小心地定义每个顶点属性之间的间隔,我们在后面会看到更多的例子(译注: 这个参数的意思简单说就是从这个属性第二次出现的地方到整个数组0位置之间有多少字节); - 最后一个参数的类型是
void*,所以需要我们进行这个奇怪的强制类型转换。它表示位置数据在缓冲中起始位置的偏移量(Offset)。由于位置数据在数组的开头,所以这里是0。我们会在后面详细解释这个参数。
每个顶点属性从一个VBO管理的内存中获得它的数据,而具体是从哪个VBO(程序中可以有多个VBO)获取则是通过在调用glVertexAttribPointer时绑定到GL_ARRAY_BUFFER的VBO决定的。由于在调用glVertexAttribPointer之前绑定的是先前定义的VBO对象,顶点属性0现在会链接到它的顶点数据。
现在我们已经定义了OpenGL该如何解释顶点数据,我们现在应该使用glEnableVertexAttribArray,以顶点属性位置值作为参数,启用顶点属性;顶点属性默认是禁用的。
自此,所有东西都已经设置好了:
- 我们使用一个顶点缓冲对象将顶点数据初始化至缓冲中;
- 建立了一个顶点和一个片段着色器;
- 告诉了OpenGL如何把顶点数据链接到顶点着色器的顶点属性上。
在OpenGL中绘制一个物体,代码会像是这样:
1 | // 0. 复制顶点数组到缓冲中供OpenGL使用 |
每当我们绘制一个物体的时候都必须重复这一过程。这看起来可能不多,但是如果有超过5个顶点属性,上百个不同物体呢(这其实并不罕见)。绑定正确的缓冲对象,为每个物体配置所有顶点属性很快就变成一件麻烦事。
有没有一些方法可以使我们把所有这些状态配置储存在一个对象中,并且可以通过绑定这个对象来恢复状态呢?
顶点数组对象
顶点数组对象(Vertex Array Object, VAO)可以像顶点缓冲对象那样被绑定,任何随后的顶点属性调用都会储存在这个VAO中。这样的好处就是,当配置顶点属性指针时,你只需要将那些调用执行一次,之后再绘制物体的时候只需要绑定相应的VAO就行了。这使在不同顶点数据和属性配置之间切换变得非常简单,只需要绑定不同的VAO就行了。
OpenGL的核心模式要求我们使用VAO,所以它知道该如何处理我们的顶点输入。如果我们绑定VAO失败,OpenGL会拒绝绘制任何东西。
一个顶点数组对象会储存以下这些内容:
- glEnableVertexAttribArray和glDisableVertexAttribArray的调用;
- 通过glVertexAttribPointer设置的顶点属性配置;
- 通过glVertexAttribPointer调用与顶点属性关联的顶点缓冲对象。
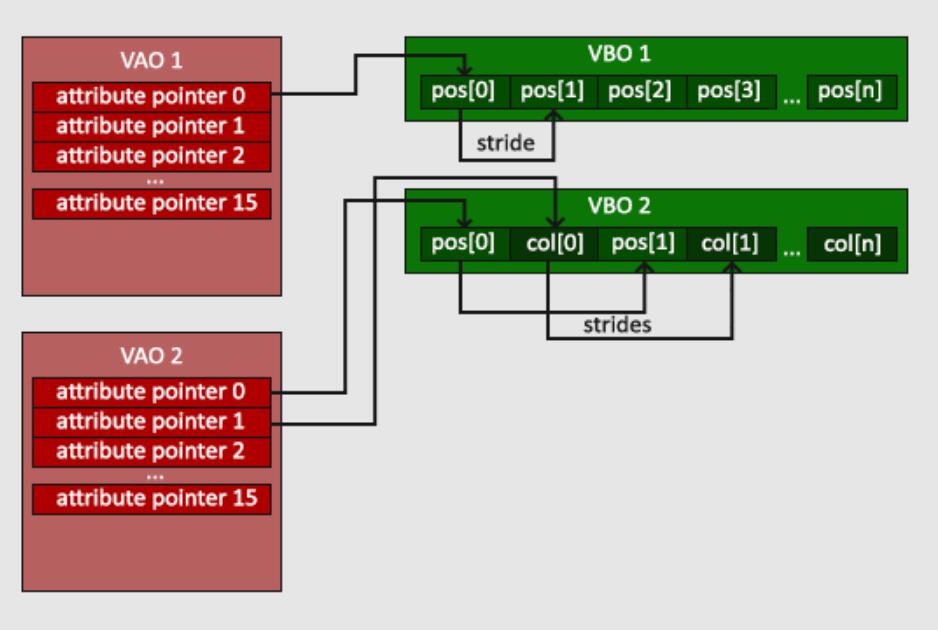
创建一个VAO和创建一个VBO很类似:
1 | unsigned int VAO; |
要想使用VAO,要做的只是使用glBindVertexArray绑定VAO。从绑定之后起,我们应该绑定和配置对应的VBO和属性指针,之后解绑VAO供之后使用。当我们打算绘制一个物体的时候,我们只要在绘制物体前简单地把VAO绑定到希望使用的设定上就行了:
1 | // ..:: 初始化代码(只运行一次 (除非你的物体频繁改变)) :: .. |
就这么多了!前面做的一切都是等待这一刻,一个储存了我们顶点属性配置和应使用的VBO的顶点数组对象。一般当你打算绘制多个物体时,你首先要生成/配置所有的VAO(和必须的VBO及属性指针)**,然后储存它们供后面使用。当我们打算绘制物体的时候就拿出相应的VAO,绑定它,绘制完物体后,再解绑VAO**。
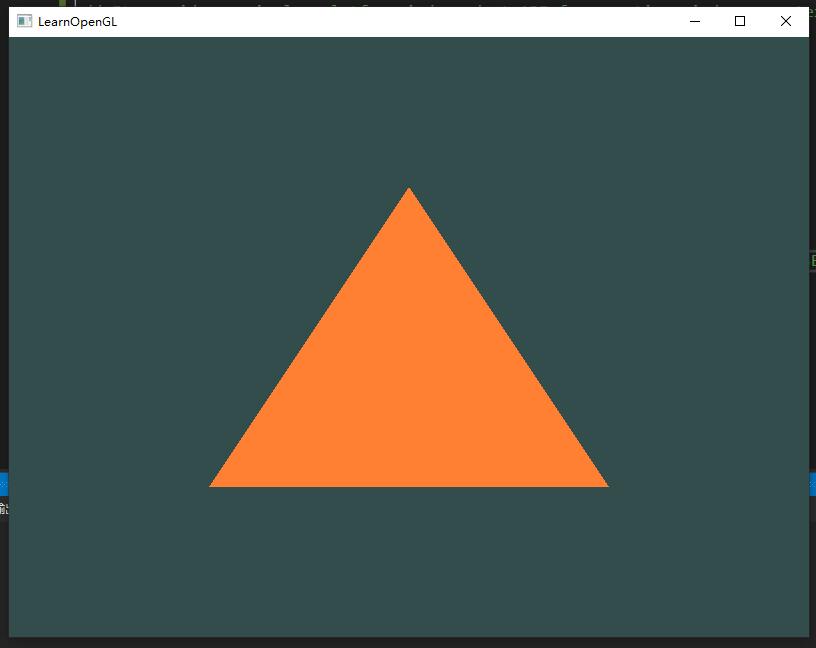
一直期待的三角形
要想绘制我们想要的物体,OpenGL给我们提供了glDrawArrays函数,它使用当前激活的着色器,之前定义的顶点属性配置,和VBO的顶点数据(通过VAO间接绑定)来绘制图元。
1 | glUseProgram(shaderProgram); |
glDrawArrays函数:
- 第一个参数是我们打算绘制的OpenGL图元的类型。由于我们在一开始时说过,我们希望绘制的是一个三角形,这里传递GL_TRIANGLES给它;
- 第二个参数指定了顶点数组的起始索引,我们这里填0;
- 最后一个参数指定我们打算绘制多少个顶点,这里是3(我们只从我们的数据中渲染一个三角形,它只有3个顶点长)。
1 | // ... 其他代码没有修改 |
索引缓冲对象
在渲染顶点这一话题上我们还有最后一个需要讨论的东西——索引缓冲对象(Element Buffer Object,EBO,也叫Index Buffer Object,IBO)。要解释索引缓冲对象的工作方式最好还是举个例子:假设我们不再绘制一个三角形而是绘制一个矩形。我们可以绘制两个三角形来组成一个矩形(OpenGL主要处理三角形)。
1 | float vertices[] = { |
可以看到,有几个顶点叠加了。我们指定了右下角和左上角两次!一个矩形只有4个而不是6个顶点,这样就产生50%的额外开销。当我们有包括上千个三角形的模型之后这个问题会更糟糕,这会产生一大堆浪费。更好的解决方案是只储存不同的顶点,并设定绘制这些顶点的顺序。这样子我们只要储存4个顶点就能绘制矩形了,之后只要指定绘制的顺序就行了。如果OpenGL提供这个功能就好了,对吧?
很幸运,索引缓冲对象的工作方式正是这样的。和顶点缓冲对象一样,EBO也是一个缓冲,它专门储存索引,OpenGL调用这些顶点的索引来决定该绘制哪个顶点。所谓的索引绘制(Indexed Drawing)正是我们问题的解决方案。
首先,我们先要定义(不重复的)顶点,和绘制出矩形所需的索引:
1 | // 顶点 |
下一步我们需要创建索引缓冲对象:
1 | unsigned int EBO; |
与VBO类似,我们先绑定EBO然后用glBufferData把索引复制到缓冲里。同样,和VBO类似,我们会把这些函数调用放在绑定和解绑函数调用之间,只不过这次我们把缓冲的类型定义为GL_ELEMENT_ARRAY_BUFFER。
1 | glBindBuffer(GL_ELEMENT_ARRAY_BUFFER, EBO); |
要注意的是,我们传递了GL_ELEMENT_ARRAY_BUFFER当作缓冲目标。最后一件要做的事是用glDrawElements来替换glDrawArrays函数,来指明我们从索引缓冲渲染。使用glDrawElements时,我们会使用当前绑定的索引缓冲对象中的索引进行绘制:
1 | glBindBuffer(GL_ELEMENT_ARRAY_BUFFER, EBO); |
glDrawElements的参数说明:
- 第一个参数指定了我们绘制的模式,这个和glDrawArrays的一样;
- 第二个参数是我们打算绘制顶点的个数,这里填6,也就是说我们一共需要绘制6个顶点;
- 第三个参数是索引的类型,这里是GL_UNSIGNED_INT;
- 最后一个参数里我们可以指定EBO中的偏移量(或者传递一个索引数组,但是这是当你不在使用索引缓冲对象的时候),但是我们会在这里填写0。
glDrawElements函数从当前绑定到GL_ELEMENT_ARRAY_BUFFER目标的EBO中获取索引。这意味着我们必须在每次要用索引渲染一个物体时绑定相应的EBO,这还是有点麻烦。不过顶点数组对象VAO同样可以保存索引缓冲对象的绑定状态。VAO绑定时正在绑定的索引缓冲对象会被保存为VAO的元素缓冲对象。绑定VAO的同时也会自动绑定EBO。
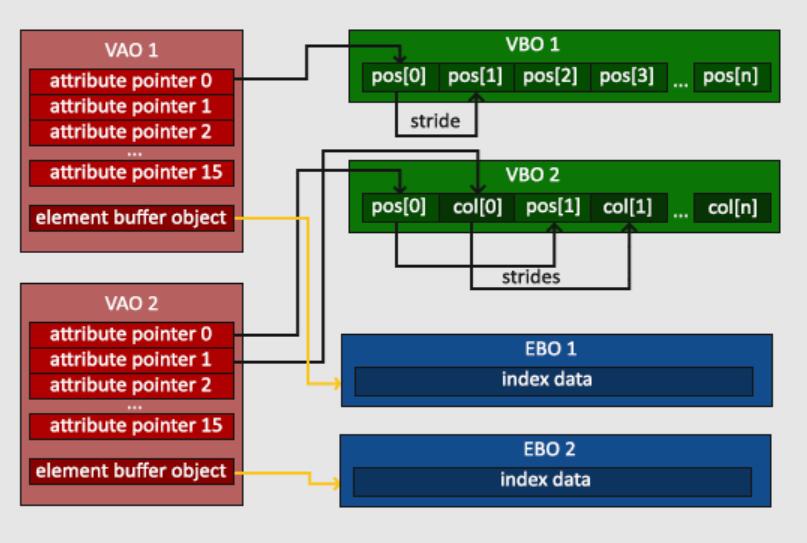
1 | // ..:: 初始化代码 :: .. |
当目标是GL_ELEMENT_ARRAY_BUFFER的时候,VAO会储存glBindBuffer的函数调用。这也意味着它也会储存解绑调用,所以确保你没有在解绑VAO之前解绑索引数组缓冲,否则它就没有这个EBO配置了。
1 | // ... 其他代码都没有修改 |
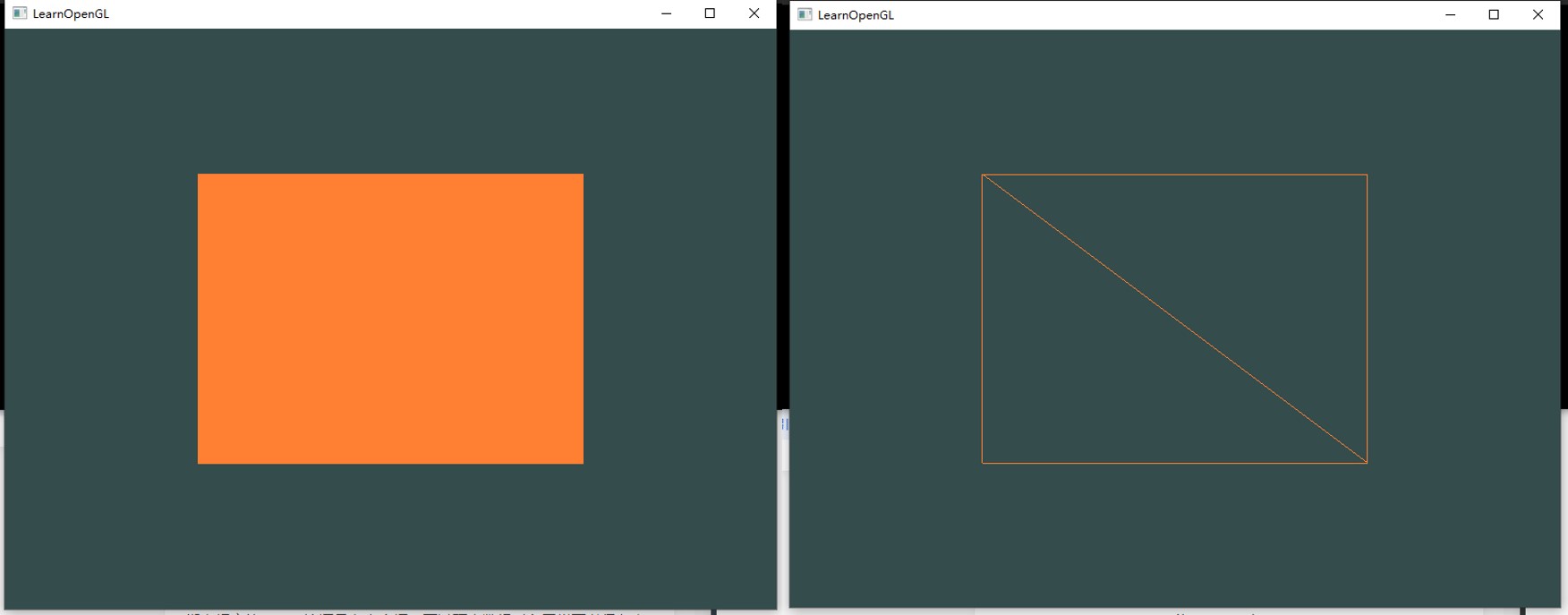
线框模式(Wireframe Mode):要想用线框模式绘制你的三角形,你可以通过glPolygonMode(GL_FRONT_AND_BACK, GL_LINE)函数配置OpenGL如何绘制图元。第一个参数表示我们打算将其应用到所有的三角形的正面和背面,第二个参数告诉我们用线来绘制。之后的绘制调用会一直以线框模式绘制三角形,直到我们用glPolygonMode(GL_FRONT_AND_BACK, GL_FILL)将其设置回默认模式。
练习题
- 添加更多顶点到数据中,使用glDrawArrays,尝试绘制两个彼此相连的三角形;
- 创建相同的两个三角形,但对它们的数据使用不同的VAO和VBO;
- 创建两个着色器程序,第二个程序使用一个不同的片段着色器,输出黄色;再次绘制这两个三角形,让其中一个输出为黄色。
(咕咕,之后再做)
着色器
从基本意义上来说,着色器只是一种把输入转化为输出的程序。着色器也是一种非常独立的程序,因为它们之间不能相互通信;它们之间唯一的沟通只有通过输入和输出。
现在我们会用一种更加广泛的形式详细解释着色器,特别是OpenGL着色器语言(GLSL)。
GLSL
着色器是使用一种叫GLSL的类C语言写成的。GLSL是为图形计算量身定制的,它包含一些针对向量和矩阵操作的有用特性。
着色器的开头总是要声明版本,接着是输入和输出变量、uniform和main函数。每个着色器的入口点都是main函数,在这个函数中我们处理所有的输入变量,并将结果输出到输出变量中。如果你不知道什么是uniform也不用担心,我们后面会进行讲解。
一个典型的着色器有下面的结构:
1 |
|
当我们特别谈论到顶点着色器的时候,每个输入变量也叫顶点属性(Vertex Attribute)。我们能声明的顶点属性是有上限的,它一般由硬件来决定。OpenGL确保至少有16个包含4分量的顶点属性可用,但是有些硬件或许允许更多的顶点属性,你可以查询GL_MAX_VERTEX_ATTRIBS来获取具体的上限:
1 | int nrAttributes; |
通常情况下它至少会返回16个,大部分情况下是够用了。
数据类型
和其他编程语言一样,GLSL有数据类型可以来指定变量的种类。GLSL中包含C等其它语言大部分的默认基础数据类型:int、float、double、uint和bool。GLSL也有两种容器类型,它们会在这个教程中使用很多,分别是向量(Vector)和矩阵(Matrix),其中矩阵我们会在之后的教程里再讨论。
向量(Vector):GLSL中的向量是一个可以包含有1、2、3或者4个分量的容器,分量的类型可以是前面默认基础类型的任意一个。它们可以是下面的形式(n代表分量的数量):
vecn:包含n个float分量的默认向量;bvecn:包含n个bool分量的向量;ivecn:包含n个int分量的向量;uvecn:包含n个unsigned int分量的向量;dvecn:包含n个double分量的向量。
大多数时候我们使用vecn,因为float足够满足大多数要求了。
一个向量的分量可以通过vec.x这种方式获取,这里x是指这个向量的第一个分量。你可以分别使用.x、.y、.z和.w来获取它们的第1、2、3、4个分量。GLSL也允许你对颜色使用rgba,或是对纹理坐标使用stpq访问相同的分量。
向量这一数据类型也允许一些有趣而灵活的分量选择方式,叫做重组(Swizzling)。重组允许这样的语法:
1 | vec2 someVec; |
你可以使用上面4个字母任意组合来创建一个和原来向量一样长的(同类型)新向量,只要原来向量有那些分量即可;然而,你不允许在一个vec2向量中去获取.z元素。我们也可以把一个向量作为一个参数传给不同的向量构造函数,以减少需求参数的数量:
1 | vec2 vect = vec2(0.5, 0.7); |
向量是一种灵活的数据类型,我们可以把用在各种输入和输出上。
输入与输出
我们希望每个着色器都有输入和输出,这样才能进行数据交流和传递。GLSL定义了in和out关键字专门来实现这个目的。每个着色器使用这两个关键字设定输入和输出,只要一个输出变量与下一个着色器阶段的输入匹配,它就会传递下去。但在顶点和片段着色器中会有点不同。
顶点着色器应该接收的是一种特殊形式的输入,否则就会效率低下。顶点着色器的输入特殊在,它从顶点数据中直接接收输入。为了定义顶点数据该如何管理,我们使用location这一元数据指定输入变量,这样我们才可以在CPU上配置顶点属性。我们已经在前面的教程看过这个了,layout (location = 0)。顶点着色器需要为它的输入提供一个额外的layout标识,这样我们才能把它链接到顶点数据。
你也可以忽略layout (location = 0)标识符,通过在OpenGL代码中使用glGetAttribLocation查询属性位置值(Location),但是我更喜欢在着色器中设置它们,这样会更容易理解而且节省你(和OpenGL)的工作量。
另一个例外是片段着色器,它需要一个vec4颜色输出变量,因为片段着色器需要生成一个最终输出的颜色。如果你在片段着色器没有定义输出颜色,OpenGL会把你的物体渲染为黑色(或白色)。
所以,如果我们打算从一个着色器向另一个着色器发送数据,我们必须在发送方着色器中声明一个输出,在接收方着色器中声明一个类似的输入。当类型和名字都一样的时候,OpenGL就会把两个变量链接到一起,它们之间就能发送数据了(这是在链接程序对象时完成的)。
为了展示这是如何工作的,我们会稍微改动一下之前教程里的那个着色器,让顶点着色器为片段着色器决定颜色。
顶点着色器:
1 |
|
片段着色器:
1 |
|
你可以看到我们在顶点着色器中声明了一个vertexColor变量作为vec4输出,并在片段着色器中声明了一个类似的vertexColor。由于它们名字相同且类型相同,片段着色器中的vertexColor就和顶点着色器中的vertexColor链接了。由于我们在顶点着色器中将颜色设置为深红色,最终的片段也是深红色的。
让我们更上一层楼,看看能否从应用程序中直接给片段着色器发送一个颜色!
Uniform
Uniform是一种从CPU中的应用向GPU中的着色器发送数据的方式,但uniform和顶点属性有些不同。首先,uniform是全局的(Global)。全局意味着uniform变量必须在每个着色器程序对象中都是独一无二的(只有一个,而不是每个着色器都有单独一个的意思),而且它可以被着色器程序的任意着色器在任意阶段访问。第二,无论你把uniform值设置成什么,uniform会一直保存它们的数据,直到它们被重置或更新。
我们可以在一个着色器中添加uniform关键字至类型和变量名前来声明一个GLSL的uniform。从此处开始我们就可以在着色器中使用新声明的uniform了。我们来看看这次是否能通过uniform设置三角形的颜色:
1 |
|
我们在片段着色器中声明了一个uniform vec4的ourColor,并把片段着色器的输出颜色设置为uniform值的内容。因为uniform是全局变量,我们可以在任何着色器中定义它们,而无需通过顶点着色器作为中介。顶点着色器中不需要这个uniform,所以我们不用在那里定义它。
如果你声明了一个uniform却在GLSL代码中没用过,编译器会静默移除这个变量,导致最后编译出的版本中并不会包含它,这可能导致几个非常麻烦的错误,记住这点!
这个uniform现在还是空的;我们还没有给它添加任何数据,所以下面我们就做这件事。我们首先需要找到着色器中uniform属性的索引/位置值。当我们得到uniform的索引/位置值后,我们就可以更新它的值了。这次我们不去给像素传递单独一个颜色,而是让它随着时间改变颜色:
1 | float timeValue = glfwGetTime(); |
首先我们通过glfwGetTime()获取运行的秒数。然后我们使用sin函数让颜色在0.0到1.0之间改变,最后将结果储存到greenValue里。
接着,我们用glGetUniformLocation查询uniform ourColor的位置值。我们为查询函数提供着色器程序和uniform的名字(这是我们希望获得的位置值的来源)。如果glGetUniformLocation返回-1就代表没有找到这个位置值。最后,我们可以通过glUniform4f函数设置uniform值。注意,查询uniform地址不要求你之前使用过着色器程序,但是更新一个uniform之前你必须先使用程序(调用glUseProgram),因为它是在当前激活的着色器程序中设置uniform的。
因为OpenGL在其核心是一个C库,所以它不支持类型重载,在函数参数不同的时候就要为其定义新的函数;glUniform是一个典型例子。这个函数有一个特定的后缀,标识设定的uniform的类型。可能的后缀有:
f:函数需要一个float作为它的值;i:函数需要一个int作为它的值;ui:函数需要一个unsigned int作为它的值;3f:函数需要3个float作为它的值;fv:函数需要一个float向量/数组作为它的值。
每当你打算配置一个OpenGL的选项时就可以简单地根据这些规则选择适合你的数据类型的重载函数。在我们的例子里,我们希望分别设定uniform的4个float值,所以我们通过glUniform4f传递我们的数据(注意,我们也可以使用fv版本,一维向量)。
现在你知道如何设置uniform变量的值了,我们可以使用它们来渲染了。如果我们打算让颜色慢慢变化,我们就要在游戏循环的每一次迭代中(所以他会逐帧改变)更新这个uniform,否则三角形就不会改变颜色。
uniform对于设置一个在渲染迭代中会改变的属性是一个非常有用的工具,它也是一个在程序和着色器间数据交互的很好工具,但假如我们打算为每个顶点设置一个颜色的时候该怎么办?这种情况下,我们就不得不声明和顶点数目一样多的uniform了。在这一问题上更好的解决方案是在顶点属性中包含更多的数据,这是我们接下来要做的事情。
更多属性
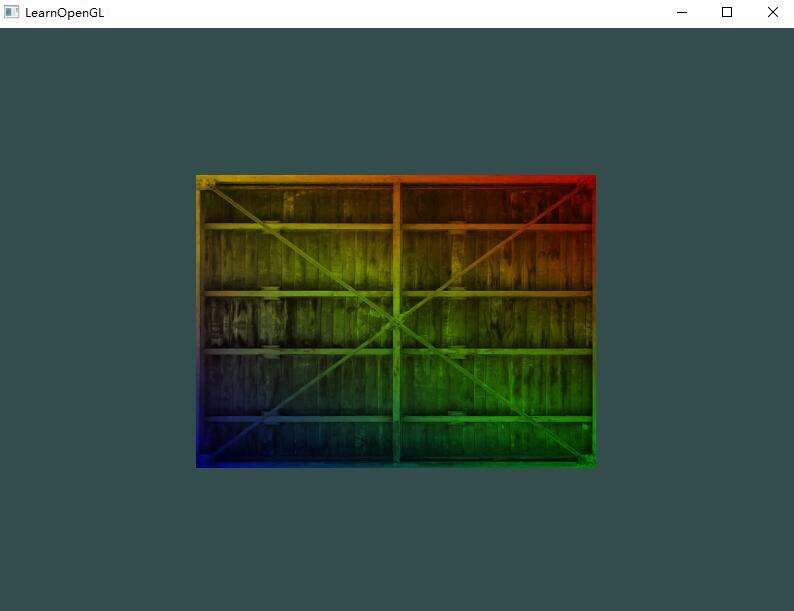
在前面的教程中,我们了解了如何填充VBO、配置顶点属性指针以及如何把它们都储存到一个VAO里。这次,我们同样打算把颜色数据加进顶点数据中。我们将把颜色数据添加为3个float值至vertices数组。我们将把三角形的三个角分别指定为红色、绿色和蓝色:
1 | float vertices[] = { |
由于现在有更多的数据要发送到顶点着色器,我们有必要去调整一下顶点着色器,使它能够接收颜色值作为一个顶点属性输入。需要注意的是我们用layout标识符来把aColor属性的位置值设置为1:
1 |
|
由于我们不再使用uniform来传递片段的颜色了,现在使用ourColor输出变量,我们必须再修改一下片段着色器:
1 |
|
因为我们添加了另一个顶点属性,并且更新了VBO的内存,我们就必须重新配置顶点属性指针。更新后的VBO内存中的数据现在看起来像这样:
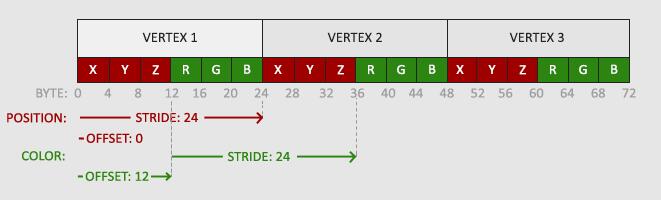
知道了现在使用的布局,我们就可以使用glVertexAttribPointer函数更新顶点格式,
1 | // 位置属性 |
glVertexAttribPointer函数的前几个参数比较明了。这次我们配置属性位置值为1的顶点属性。颜色值有3个float那么大,我们不去标准化这些值。
由于我们现在有了两个顶点属性,我们不得不重新计算步长值。为获得数据队列中下一个属性值(比如位置向量的下个x分量)我们必须向右移动6个float,其中3个是位置值,另外3个是颜色值。这使我们的步长值为6乘以float的字节数**(=24字节)。
同样,这次我们必须指定一个偏移量。对于每个顶点来说,位置顶点属性在前,所以它的偏移量是0。颜色属性紧随位置数据之后,所以偏移量就是3 * sizeof(float),用字节来计算就是12字节。
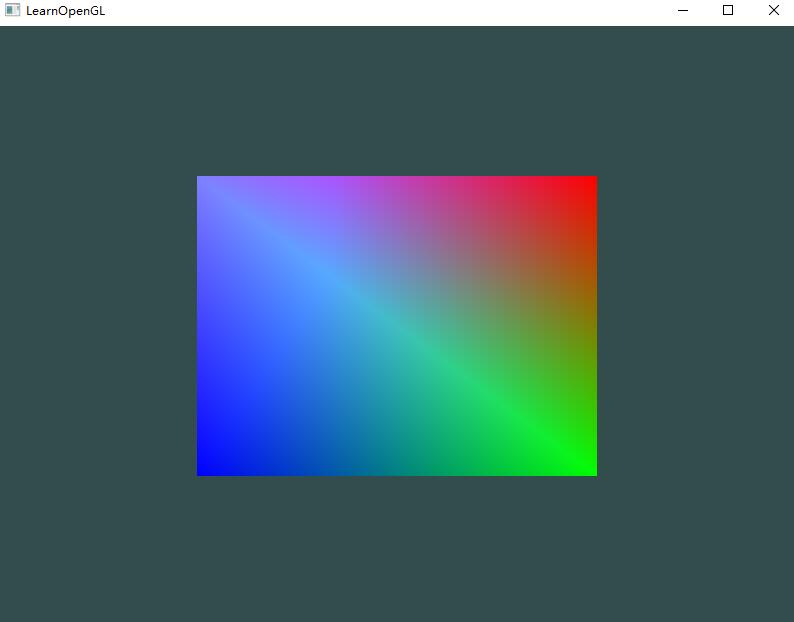
这个图片可能不是你所期望的那种,因为我们只提供了3个颜色,而不是我们现在看到的大调色板。这是在片段着色器中进行的所谓片段插值(Fragment Interpolation)的结果。当渲染一个三角形时,光栅化(Rasterization)阶段通常会造成比原指定顶点更多的片段。光栅会根据每个片段在三角形形状上所处相对位置决定这些片段的位置(属性?)。
我们自己的着色器类
编写、编译、管理着色器是件麻烦事。在着色器主题的最后,我们会写一个类来让我们的生活轻松一点,它可以从硬盘读取着色器,然后编译并链接它们,并对它们进行错误检测,这就变得很好用了。这也会让你了解该如何封装目前所学的知识到一个抽象对象中。
我们会把着色器类全部放在在头文件里,主要是为了学习用途,当然也方便移植。我们先来添加必要的include,并定义类结构:
1 |
|
在上面,我们在头文件顶部使用了几个预处理指令(Preprocessor Directives)。这些预处理指令(#ifndef SHADER_H)会告知你的编译器只在它没被包含过的情况下才包含和编译这个头文件,即使多个文件都包含了这个着色器头文件。它是用来防止链接冲突的。
着色器类储存了着色器程序的ID。它的构造器需要顶点和片段着色器源代码的文件路径,这样我们就可以把源码的文本文件储存在硬盘上了。除此之外,为了让我们的生活更轻松一点,还加入了一些工具函数:use用来激活着色器程序,所有的set…函数能够查询一个unform的位置值并设置它的值。
从文件读取
我们使用C++文件流读取着色器内容,储存到几个string对象里:
1 | // 构造器读取并构建着色器 |
下一步,我们需要编译和链接着色器。注意,我们也将检查编译/链接是否失败,如果失败则打印编译时错误,调试的时候这些错误输出会及其重要(你总会需要这些错误日志的):
1 | // 构造器读取并构建着色器 |
use函数非常简单:
1 | // 使用/激活程序 |
uniform的setter函数也很类似:
1 | // uniform工具函数 |
现在我们就写完了一个完整的着色器类。使用这个着色器类很简单;只要创建一个着色器对象,从那一点开始我们就可以开始使用了:
1 | // ... GLFW GLAD初始化 |
我们把顶点和片段着色器储存为两个叫做shader.vs和shader.fs的文件。你可以使用自己喜欢的名字命名着色器文件;我自己觉得用.vs和.fs作为扩展名很直观。
纹理
我们已经了解到,我们可以为每个顶点添加颜色来增加图形的细节,从而创建出有趣的图像。但是,如果想让图形看起来更真实,我们就必须有足够多的顶点,从而指定足够多的颜色。这将会产生很多额外开销,因为每个模型都会需求更多的顶点,每个顶点又需求一个颜色属性。
艺术家和程序员更喜欢使用纹理(Texture)。纹理是一个2D图片(甚至也有1D和3D的纹理),它可以用来添加物体的细节;你可以想象纹理是一张绘有砖块的纸,无缝折叠贴合到你的3D的房子上,这样你的房子看起来就像有砖墙外表了。因为我们可以在一张图片上插入非常多的细节,这样就可以让物体非常精细而不用指定额外的顶点。
除了图像以外,纹理也可以被用来储存大量的数据,这些数据可以发送到着色器上(例如纹理深度信息),但是这不是我们现在的主题。
为了能够把纹理映射(Map)到三角形上,我们需要指定三角形的每个顶点各自对应纹理的哪个部分。这样每个顶点就会关联着一个纹理坐标(Texture Coordinate),用来标明该从纹理图像的哪个部分采样(译注:采集片段颜色)。之后在图形的其它片段上进行片段插值(Fragment Interpolation)(插值纹理坐标)。
纹理坐标在x和y轴上,范围为0到1之间(注意我们使用的是2D纹理图像)。使用纹理坐标获取纹理颜色叫做采样(Sampling)。纹理坐标起始于(0, 0),也就是纹理图片的左下角,终于(1, 1),即纹理图片的右上角。下面的图片展示了我们是如何把纹理坐标映射到三角形上的。
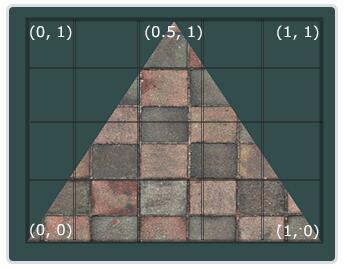
我们为三角形指定了3个纹理坐标点。如上图所示,我们希望三角形的左下角对应纹理的左下角,因此我们把三角形左下角顶点的纹理坐标设置为(0, 0);三角形的上顶点对应于图片的上中位置所以我们把它的纹理坐标设置为(0.5, 1.0);同理右下方的顶点设置为(1, 0)。我们只要给顶点着色器传递这三个纹理坐标就行了,接下来它们会被传片段着色器中,它会为每个片段进行纹理坐标的插值。
纹理坐标看起来就像这样:
1 | float texCoords[] = { |
对纹理采样的解释非常宽松,它可以采用几种不同的插值方式。所以我们需要自己告诉OpenGL该怎样对纹理采样。
纹理环绕方式
纹理坐标的范围通常是从(0, 0)到(1, 1),那如果我们把纹理坐标设置在范围之外会发生什么?OpenGL默认的行为是重复这个纹理图像(我们基本上忽略浮点纹理坐标的整数部分),但OpenGL提供了更多的选择:
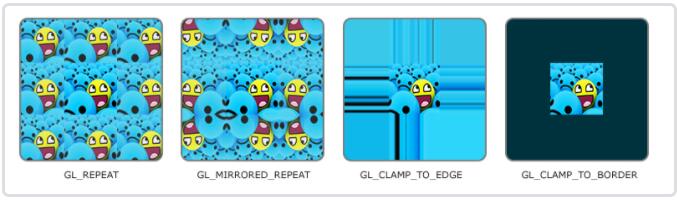
GL_REPEAT:对纹理的默认行为。重复纹理图像;GL_MIRRORED_REPEAT:和GL_REPEAT一样,但每次重复图片是镜像放置的;GL_CLAMP_TO_EDGE:纹理坐标会被约束在0到1之间,超出的部分会重复纹理坐标的边缘,产生一种边缘被拉伸的效果;GL_CLAMP_TO_BORDER:超出的坐标为用户指定的边缘颜色。
当纹理坐标超出默认范围时,每个选项都有不同的视觉效果输出。我们来看看这些纹理图像的例子:
前面提到的每个选项都可以使用glTexParameter*函数(*不是指针,是不同类型的重载,看后面代码就知道了)对单独的一个坐标轴(str)设置(s、t(如果是使用3D纹理那么还有一个r)它们和x、y、z是等价的):
1 | glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_MIRRORED_REPEAT); |
- 第一个参数指定了纹理目标;我们使用的是2D纹理,因此纹理目标是GL_TEXTURE_2D;
- 第二个参数需要我们指定设置的选项与应用的纹理轴。我们打算配置的是WRAP选项,并且指定S和T轴;
- 最后一个参数需要我们传递一个环绕方式(Wrapping),在这个例子中OpenGL会给当前激活的纹理设定纹理环绕方式为GL_MIRRORED_REPEAT。
如果我们选择GL_CLAMP_TO_BORDER选项,我们还需要指定一个边缘的颜色。这需要使用glTexParameter函数的fv后缀形式(float vector),用GL_TEXTURE_BORDER_COLOR作为它的选项,并且传递一个float数组作为边缘的颜色值:
1 | float borderColor[] = { 1.0f, 1.0f, 0.0f, 1.0f }; |
纹理过滤
纹理坐标不依赖于分辨率(Resolution),它可以是任意浮点值,所以OpenGL需要知道怎样将纹理像素(Texture Pixel,也叫Texel,译注1)映射到纹理坐标。
当你有一个很大的物体但是纹理的分辨率很低的时候这就变得很重要了。你可能已经猜到了,OpenGL也有对于纹理过滤(Texture Filtering)的选项。纹理过滤有很多个选项,但是现在我们只讨论最重要的两种:GL_NEAREST和GL_LINEAR。
Texture Pixel也叫Texel,你可以想象你打开一张.jpg格式图片,不断放大你会发现它是由无数像素点组成的,这个点就是纹理像素;注意不要和纹理坐标搞混,纹理坐标是你给模型顶点设置的那个数组,OpenGL以这个顶点的纹理坐标数据去查找纹理图像上的像素,然后进行采样提取纹理像素的颜色。
GL_NEAREST(也叫邻近过滤,Nearest Neighbor Filtering)是OpenGL默认的纹理过滤方式。当设置为GL_NEAREST的时候,OpenGL会选择中心点最接近纹理坐标的那个像素。下图中你可以看到四个像素,加号代表纹理坐标。左上角那个纹理像素的中心距离纹理坐标最近,所以它会被选择为样本颜色:

GL_LINEAR(也叫线性过滤,(Bi)linear Filtering)它会基于纹理坐标附近的纹理像素,计算出一个插值,近似出这些纹理像素之间的颜色。一个纹理像素的中心距离纹理坐标越近,那么这个纹理像素的颜色对最终的样本颜色的贡献越大。下图中你可以看到返回的颜色是邻近像素的混合色:
那么这两种纹理过滤方式有怎样的视觉效果呢?让我们看看在一个很大的物体上应用一张低分辨率的纹理会发生什么吧(纹理被放大了,每个纹理像素都能看到):

GL_NEAREST产生了颗粒状的图案,我们能够清晰看到组成纹理的像素,而GL_LINEAR能够产生更平滑的图案,很难看出单个的纹理像素(但是变得有点模糊了)。GL_LINEAR可以产生更真实的输出,但有些开发者更喜欢8-bit风格,所以他们会用GL_NEAREST选项。
当进行放大(Magnify)和缩小(Minify)操作的时候可以设置纹理过滤的选项,比如你可以在纹理被缩小的时候使用邻近过滤,被放大时使用线性过滤。我们需要使用glTexParameter*函数为放大和缩小指定过滤方式。这段代码看起来会和纹理环绕方式的设置很相似:
1 | glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_NEAREST); |
多级渐远纹理
假设我们有一个包含着上千物体的大房间,每个物体上都有纹理。有些物体会很远,但其纹理会拥有与近处物体同样高的分辨率。由于远处的物体可能只产生很少的片段,OpenGL从高分辨率纹理中为这些片段获取正确的颜色值就很困难,因为它需要对一个跨过纹理很大部分的片段只拾取一个纹理颜色。在小物体上这会产生不真实的感觉,更不用说对它们使用高分辨率纹理浪费内存的问题了。
OpenGL使用一种叫做多级渐远纹理(Mipmap)的概念来解决这个问题,它简单来说就是一系列的纹理图像,后一个纹理图像是前一个的二分之一(宽高同时二分之一,总面积四分之一)。多级渐远纹理背后的理念很简单:距观察者的距离超过一定的阈值,OpenGL会使用不同的多级渐远纹理,即最适合物体的距离的那个。由于距离远,解析度不高也不会被用户注意到。同时,多级渐远纹理另一加分之处是它的性能非常好。让我们看一下多级渐远纹理是什么样子的:

手工为每个纹理图像创建一系列多级渐远纹理很麻烦,幸好OpenGL有一个glGenerateMipmaps函数,在创建完一个纹理后调用它,OpenGL就会承担接下来的所有工作了。
在渲染中切换多级渐远纹理级别(Level)时,OpenGL在两个不同级别的多级渐远纹理层之间会产生不真实的生硬边界。就像普通的纹理过滤一样,切换多级渐远纹理级别时你也可以在两个不同多级渐远纹理级别之间使用NEAREST和LINEAR过滤。
为了指定不同多级渐远纹理级别之间的过滤方式,你可以使用下面四个选项中的一个代替原有的过滤方式:
GL_NEAREST_MIPMAP_NEAREST:使用最邻近的多级渐远纹理来匹配像素大小,并使用邻近插值进行纹理采样;GL_LINEAR_MIPMAP_NEAREST:使用最邻近的多级渐远纹理级别,并使用线性插值进行采样;GL_NEAREST_MIPMAP_LINEAR:在两个最匹配像素大小的多级渐远纹理之间进行线性插值,使用邻近插值进行采样;GL_LINEAR_MIPMAP_LINEAR:在两个邻近的多级渐远纹理之间使用线性插值,并使用线性插值进行采样。
就像纹理过滤一样,我们可以使用glTexParameteri将过滤方式设置为前面四种提到的方法之一:
1 | glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_LINEAR_MIPMAP_LINEAR); |
一个常见的错误是,将放大过滤的选项设置为多级渐远纹理过滤选项之一。这样没有任何效果,因为多级渐远纹理主要是使用在纹理被缩小的情况下的:纹理放大不会使用多级渐远纹理,为放大过滤设置多级渐远纹理的选项会产生一个GL_INVALID_ENUM错误代码。
加载与创建纹理
使用纹理之前要做的第一件事是把它们加载到我们的应用中。纹理图像可能被储存为各种各样的格式,每种都有自己的数据结构和排列,所以我们如何才能把这些图像加载到应用中呢?一个解决方案是选一个需要的文件格式,比如.PNG,然后自己写一个图像加载器,把图像转化为字节序列。写自己的图像加载器虽然不难,但仍然挺麻烦的,而且如果要支持更多文件格式呢?你就不得不为每种你希望支持的格式写加载器了。
另一个解决方案也许是一种更好的选择,使用一个支持多种流行格式的图像加载库来为我们解决这个问题。比如说我们要用的stb_image.h库。
stb_image.h是Sean Barrett的一个非常流行的单头文件图像加载库,它能够加载大部分流行的文件格式,并且能够很简单得整合到你的工程之中。下载这一个头文件,将它以stb_image.h的名字加入你的工程,并另创建一个新的C++文件,输入以下代码:
1 |
通过定义STB_IMAGE_IMPLEMENTATION,预处理器会修改头文件,让其只包含相关的函数定义源码,等于是将这个头文件变为一个 .cpp 文件了。现在只需要在你的程序中包含stb_image.h并编译就可以了。
下面的教程中,我们会使用一张木箱的图片。要使用stb_image.h加载图片,我们需要使用它的stbi_load函数:
1 | int width, height, nrChannels; |
这个函数首先接受一个图像文件的位置作为输入。接下来它需要三个int作为它的第二、第三和第四个参数,stb_image.h将会用图像的宽度、高度和颜色通道的个数填充这三个变量。我们之后生成纹理的时候会用到的图像的宽度和高度的。
生成纹理
和之前生成的OpenGL对象一样,纹理也是使用ID引用的。让我们来创建一个:
1 | unsigned int texture; |
glGenTextures函数首先需要输入生成纹理的数量(本例子中是1),然后把它们储存在第二个参数的unsigned int数组中(我们的例子中只是单独的一个unsigned int),就像其他对象一样,我们需要绑定它,让之后任何的纹理指令都可以配置当前绑定的纹理:
1 | glBindTexture(GL_TEXTURE_2D, texture); |
现在纹理已经绑定了,我们可以使用前面载入的图片数据生成一个纹理了。纹理可以通过glTexImage2D来生成:
1 | glTexImage2D(GL_TEXTURE_2D, 0, GL_RGB, width, height, 0, GL_RGB, GL_UNSIGNED_BYTE, data); |
glTexImage2D参数不少,所以我们一个一个地讲解:
- 第一个参数指定了纹理目标(Target)。设置为GL_TEXTURE_2D意味着会生成与当前绑定的纹理对象在同一个目标上的纹理(任何绑定到GL_TEXTURE_1D和GL_TEXTURE_3D的纹理不会受到影响);
- 第二个参数为纹理指定多级渐远纹理的级别,如果你希望单独手动设置每个多级渐远纹理的级别的话。这里我们填0,也就是基本级别。
- 第三个参数告诉OpenGL我们希望把纹理储存为何种格式。我们的图像只有RGB值,因此我们也把纹理储存为RGB值。
- 第四个和第五个参数设置最终的纹理的宽度和高度。我们之前加载图像的时候储存了它们,所以我们使用对应的变量;
- 第六个参数总是被设置为0(历史遗留的问题);
- 第七第八个参数定义了源图的格式和数据类型。我们使用RGB值加载这个图像,并把它们储存为
char(byte)数组,我们将会传入对应值; - 最后一个参数是真正的图像数据(之前stbi_load加载的图像数据,
unsigned char* data)。
当调用glTexImage2D时,当前绑定的纹理对象就会被附加上纹理图像。然而,目前只有基本级别(Base-level)的纹理图像被加载了,如果要使用多级渐远纹理,我们必须手动设置所有不同的图像(不断递增第二个参数)。或者,直接在生成纹理之后调用glGenerateMipmap。这会为当前绑定的纹理自动生成所有需要的多级渐远纹理。
生成了纹理和相应的多级渐远纹理后,释放图像的内存是一个很好的习惯。
1 | stbi_image_free(data); |
生成一个纹理的过程应该看起来像这样:
1 | unsigned int texture; |
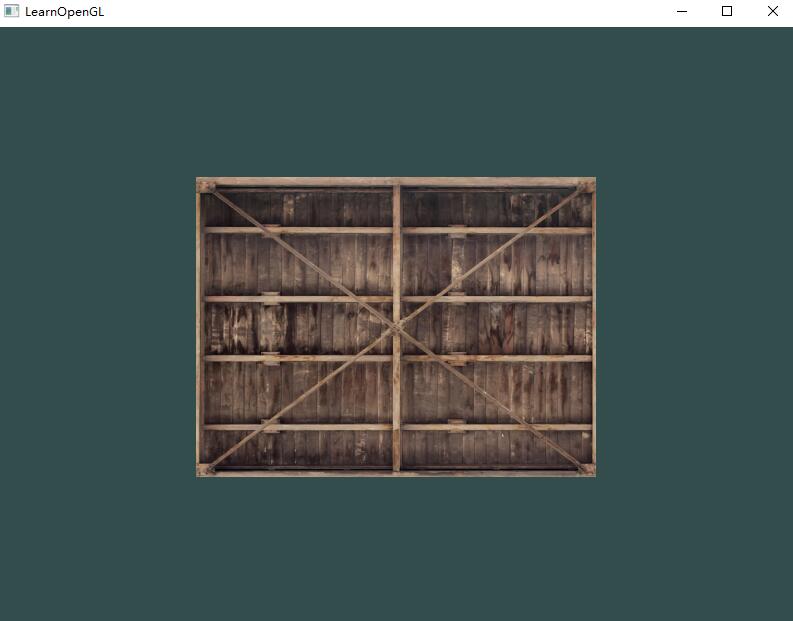
应用纹理
后面的这部分我们会使用glDrawElements绘制「你好,三角形」教程最后一部分的矩形。我们需要告知OpenGL如何采样纹理,所以我们必须使用纹理坐标更新顶点数据:
1 | float vertices[] = { |
由于我们添加了一个额外的顶点属性,我们必须告诉OpenGL我们新的顶点格式:
1 | glVertexAttribPointer(2, 2, GL_FLOAT, GL_FALSE, 8 * sizeof(float), (void*)(6 * sizeof(float))); |
注意,我们同样需要调整前面两个顶点属性的步长参数为8 * sizeof(float)。
接着我们需要调整顶点着色器使其能够接受顶点坐标为一个顶点属性,并把坐标传给片段着色器:
1 |
|
片段着色器应该接下来会把输出变量TexCoord作为输入变量。
片段着色器也应该能访问纹理对象,但是我们怎样能把纹理对象传给片段着色器呢?GLSL有一个供纹理对象使用的内建数据类型,叫做采样器(Sampler),它以纹理类型作为后缀,比如sampler1D、sampler3D,或在我们的例子中的sampler2D。我们可以简单声明一个uniform sampler2D把一个纹理添加到片段着色器中,稍后我们会把纹理赋值给这个uniform。
1 |
|
我们使用GLSL内建的texture函数来采样纹理的颜色,它第一个参数是纹理采样器,第二个参数是对应的纹理坐标。texture函数会使用之前设置的纹理参数对相应的颜色值进行采样。这个片段着色器的输出就是纹理的(插值)纹理坐标上的(过滤后的)颜色。
现在只剩下在调用glDrawElements之前绑定纹理了,它会自动把纹理赋值给片段着色器的采样器:
1 | glBindTexture(GL_TEXTURE_2D, texture); |
我们还可以把得到的纹理颜色与顶点颜色混合,来获得更有趣的效果。我们只需把纹理颜色与顶点颜色在片段着色器中相乘来混合二者的颜色:
1 | FragColor = texture(ourTexture, TexCoord) * vec4(ourColor, 1.0); |
纹理单元
你可能会奇怪为什么sampler2D变量是个uniform,我们却不用glUniform给它赋值。使用glUniform1i,我们可以给纹理采样器分配一个位置值,这样的话我们能够在一个片段着色器中设置多个纹理。一个纹理的位置值通常称为一个纹理单元(Texture Unit)。一个纹理的默认纹理单元是0,它是默认的激活纹理单元,所以教程前面部分我们没有分配一个位置值。
纹理单元的主要目的是让我们在着色器中可以使用多于一个的纹理。通过把纹理单元赋值给采样器,我们可以一次绑定多个纹理,只要我们首先激活对应的纹理单元。就像glBindTexture一样,我们可以使用glActiveTexture激活纹理单元,传入我们需要使用的纹理单元:
1 | glActiveTexture(GL_TEXTURE0); // 在绑定纹理之前先激活纹理单元 |
激活纹理单元之后,接下来的glBindTexture函数调用会绑定这个纹理到当前激活的纹理单元,纹理单元GL_TEXTURE0默认总是被激活,所以我们在前面的例子里当我们使用glBindTexture的时候,无需激活任何纹理单元。
OpenGL至少保证有16个纹理单元供你使用,也就是说你可以激活从GL_TEXTURE0到GL_TEXTRUE15。它们都是按顺序定义的,所以我们也可以通过GL_TEXTURE0 + 8的方式获得GL_TEXTURE8,这在当我们需要循环一些纹理单元的时候会很有用。
我们仍然需要编辑片段着色器来接收另一个采样器。这应该相对来说非常直接了:
1 |
|
最终输出颜色现在是两个纹理的结合。GLSL内建的mix函数需要接受两个值作为参数,并对它们根据第三个参数进行线性插值。如果第三个值是0.0,它会返回第一个输入;如果是1.0,会返回第二个输入值。0.2会返回80%的第一个输入颜色和20%的第二个输入颜色,即返回两个纹理的混合色。
我们现在需要载入并创建另一个纹理;你应该对这些步骤很熟悉了。记得创建另一个纹理对象,载入图片,使用glTexImage2D生成最终纹理。对于第二个纹理我们使用一张你学习OpenGL时的面部表情图片(草)。
为了使用第二个纹理(以及第一个),我们必须改变一点渲染流程,先绑定两个纹理到对应的纹理单元,然后定义哪个uniform采样器对应哪个纹理单元:
1 | glActiveTexture(GL_TEXTURE0); |
我们还要通过使用glUniform1i设置每个采样器的方式告诉OpenGL每个着色器采样器属于哪个纹理单元。我们只需要设置一次即可,所以这个会放在渲染循环的前面:
1 | ourShader.use(); // 不要忘记在设置uniform变量之前激活着色器程序! |
通过使用glUniform1i设置采样器,我们保证了每个uniform采样器对应着正确的纹理单元。你应该能得到下面的结果:
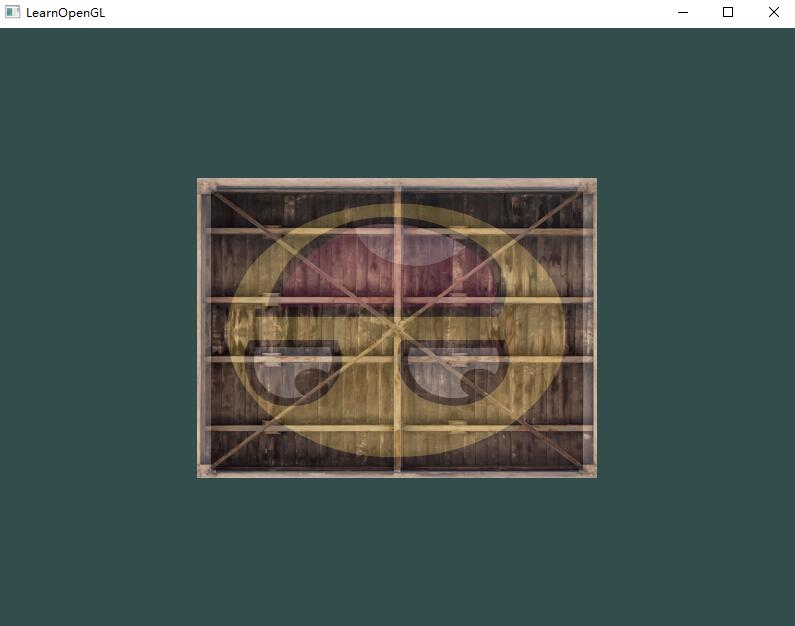
你可能注意到纹理上下颠倒了!这是因为OpenGL要求y轴0.0坐标是在图片的底部的,但是图片的y轴0.0坐标通常在顶部。很幸运,stb_image.h能够在图像加载时帮助我们翻转y轴,只需要在加载任何图像前加入以下语句即可:
1 | stbi_set_flip_vertically_on_load(true); |
在让stb_image.h在加载图片时翻转y轴之后你就应该能够获得下面的结果了:
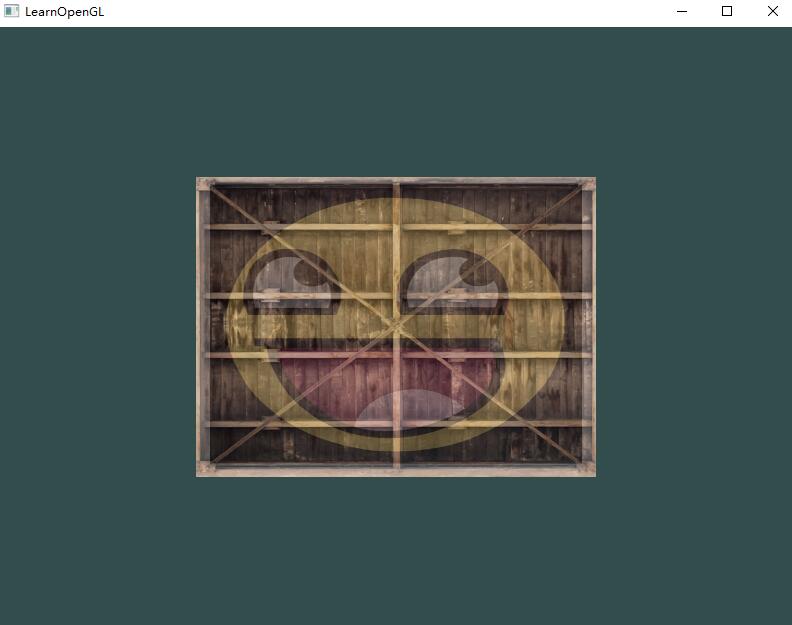
练习题
- 修改片段着色器,仅让笑脸图案朝另一个方向看;
- 尝试用不同的纹理环绕方式,设定一个从0.0f到2.0f范围内的(而不是原来的0.0f到1.0f)纹理坐标。试试看能不能在箱子的角落放置4个笑脸:参考解答,结果。记得一定要试试其它的环绕方式;
- 尝试在矩形上只显示纹理图像的中间一部分,修改纹理坐标,达到能看见单个的像素的效果。尝试使用GL_NEAREST的纹理过滤方式让像素显示得更清晰;
- 使用一个uniform变量作为mix函数的第三个参数来改变两个纹理可见度,使用上和下键来改变箱子或笑脸的可见度。
变换
尽管我们现在已经知道了如何创建一个物体、着色、加入纹理,给它们一些细节的表现,但因为它们都还是静态的物体,仍是不够有趣。我们可以尝试着在每一帧改变物体的顶点并且重配置缓冲区从而使它们移动,但这太繁琐了,而且会消耗很多的处理时间。
矩阵(Matrix)对象可以更好的变换(Transform)一个物体。当然,这并不是说我们会去讨论武术和数字虚拟世界(译注:Matrix同样也是电影「黑客帝国」的英文名,电影中人类生活在数字虚拟世界,主角(基努·里维斯)会武术)(草)。
为了深入了解变换,我们首先要在讨论矩阵之前进一步了解一下向量。这一节的目标是让你拥有将来需要的最基础的数学背景知识。如果你发现这节十分困难,尽量尝试去理解它们,当你以后需要它们的时候回过头来复习这些概念。
向量
向量最基本的定义就是一个方向。或者更正式的说,向量有一个方向(Direction)和大小(Magnitude,也叫做强度或长度)。向量可以在任意维度(Dimension)上,但是我们通常只使用2至4维。如果一个向量有2个维度,它表示一个平面的方向(想象一下2D的图像),当它有3个维度的时候它可以表达一个3D世界的方向。
由于向量是一个方向,所以有些时候会很难形象地将它们用位置(Position)表示出来。为了让其更为直观,我们通常设定这个方向的原点为(0, 0, 0),然后指向一个方向,对应一个点,使其变为位置向量(Position Vector)(你也可以把起点设置为其他的点,然后说:这个向量从这个点起始指向另一个点)。
注意,数学上是没有向量与标量相加这个运算的,但是很多线性代数的库都对它有支持(比如说我们用的GLM)。如果你使用过numpy的话,可以把它理解为Broadcasting。
我们使用**勾股定理(**Pythagoras Theorem)来获取向量的长度(Length)/大小(Magnitude)。
有一个特殊类型的向量叫做单位向量(Unit Vector)。单位向量有一个特别的性质——它的长度是1。我们可以用任意向量的每个分量除以向量的长度得到它的单位向量。我们把这种方法叫做一个向量的标准化(Normalizing)。单位向量头上有一个^样子的记号。
在相乘的时候我们有两种特定情况可以选择:一个是点乘(Dot Product),记作v⋅k,另一个是叉乘(Cross Product),记作v×k。
两个向量的点乘等于它们的数乘结果乘以两个向量之间夹角的余弦值。使用点乘可以很容易测试两个向量是否正交(Orthogonal)或平行(正交意味着两个向量互为直角)。你也可以通过点乘的结果计算两个非单位向量的夹角,点乘的结果除以两个向量的长度之积,得到的结果就是夹角的余弦值,即cosθ。点乘是通过将对应分量逐个相乘,然后再把所得积相加来计算的。
叉乘只在3D空间中有定义,它需要两个不平行向量作为输入,生成一个正交于两个输入向量的第三个向量。如果输入的两个向量也是正交的,那么叉乘之后将会产生3个互相正交的向量。
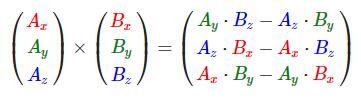
矩阵
矩阵中每一项叫做矩阵的元素(Element)。
矩阵可以通过(i, j)进行索引,i是行,j是列。矩阵有几个运算,分别是:矩阵加法、减法和乘法。
矩阵与标量之间的加减要处理到每一个元素上,和向量类似。
注意,数学上是没有矩阵与标量相加减的运算的,但是很多线性代数的库都对它有支持(比如说我们用的GLM)。如果你使用过numpy的话,可以把它理解为Broadcasting。
矩阵与矩阵之间的加减就是两个矩阵对应元素的加减运算,所以总体的规则和与标量运算是差不多的,只不过在相同索引下的元素才能进行运算。这也就是说加法和减法只对同维度的矩阵才是有定义的。
和矩阵与标量的加减一样,矩阵与标量之间的乘法也是矩阵的每一个元素分别乘以该标量。现在我们也就能明白为什么这些单独的数字要叫做标量(Scalar)了。简单来说,标量就是用它的值缩放(Scale)矩阵的所有元素(译注:注意Scalar是由Scale + -ar演变过来的)。
矩阵之间的乘法不见得有多复杂,但的确很难让人适应。矩阵乘法基本上意味着遵照规定好的法则进行相乘。当然,相乘还有一些限制:
- 只有当左侧矩阵的列数与右侧矩阵的行数相等,两个矩阵才能相乘;
- 矩阵相乘不遵守交换律(Commutative),也就是说A⋅B≠B⋅A。
假设A ⋅ B = C,那么Cij的值为A矩阵的第i行向量与B矩阵的第j列向量的点积结果,这基本上就是矩阵乘法的内核。
矩阵与向量相乘
目前为止,通过这些教程我们已经相当了解向量了。我们用向量来表示位置,表示颜色,甚至是纹理坐标。如果我们有一个M×N维矩阵,我们可以用这个矩阵乘以我们的N×1向量,因为这个矩阵的列数等于向量的行数,所以它们就能相乘。
单位矩阵
在OpenGL中,由于某些原因(齐次坐标系,为了能够方便地在变换矩阵中加入平移变换)我们通常使用4×4的变换矩阵,而其中最重要的原因就是大部分的向量都是4分量的。我们能想到的最简单的变换矩阵就是单位矩阵(Identity Matrix)。这种变换矩阵使一个向量完全不变。
缩放
对一个向量进行缩放(Scaling)就是对向量的长度进行缩放,而保持它的方向不变。由于我们进行的是2维或3维操作,我们可以分别定义一个有2或3个缩放变量的向量,每个变量缩放一个轴(x、y或z)。
不均匀(Non-uniform)缩放,因为每个轴的缩放因子(Scaling Factor)都不一样。如果每个轴的缩放因子都一样那么就叫均匀缩放(Uniform Scale)。
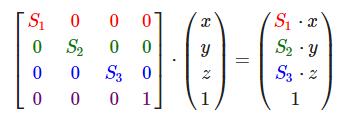
注意,第四个缩放向量仍然是1,因为在3D空间中缩放w分量是无意义的。w分量另有其他用途,在后面我们会看到。
位移
位移(Translation)是在原始向量的基础上加上另一个向量从而获得一个在不同位置的新向量的过程,从而在位移向量基础上移动了原始向量。
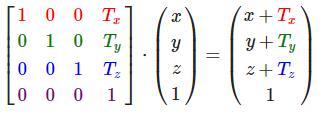
齐次坐标(Homogeneous Coordinates):向量的w分量也叫齐次坐标。想要从齐次向量得到3D向量,我们可以把x、y和z坐标分别除以w坐标。我们通常不会注意这个问题,因为w分量通常是1.0。使用齐次坐标有几点好处:它允许我们在3D向量上进行位移(如果没有w分量我们是不能位移向量的),而且下一章我们会用w值创建3D视觉效果。如果一个向量的齐次坐标是0,这个坐标就是方向向量(Direction Vector),因为w坐标是0,这个向量就不能位移(译注:这也就是我们说的不能位移一个方向)。
旋转
首先我们来定义一个向量的旋转到底是什么。2D或3D空间中的旋转用角(Angle)来表示。角可以是角度制或弧度制的,周角是360角度或2PI弧度。我个人更喜欢用角度,因为它们看起来更直观。
大多数旋转函数需要用弧度制的角,但幸运的是角度制的角也可以很容易地转化为弧度制的:
- 弧度转角度:
角度 = (弧度 / PI) * 180.0f; - 角度转弧度:
弧度 = (角度 / 180.0f) * PI。
PI约等于3.14159265359。
在3D空间中旋转需要定义一个角和一个旋转轴(Rotation Axis),物体会沿着给定的旋转轴旋转特定角度。
旋转矩阵在3D空间中每个单位轴都有不同定义,旋转角度用θ表示。
沿x轴旋转:
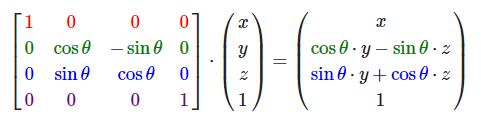
沿y轴旋转:
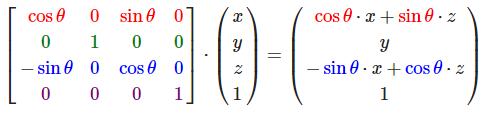
沿z轴旋转:
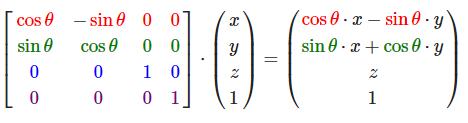
利用旋转矩阵我们可以把任意位置向量沿一个单位旋转轴进行旋转。也可以将多个矩阵复合,比如先沿着x轴旋转再沿着y轴旋转。但是这会很快导致一个问题——万向节死锁(Gimbal Lock)。在这里我们不会讨论它的细节,但是对于3D空间中的旋转,一个更好的模型是沿着任意的一个轴,而不是对一系列旋转矩阵进行复合。样的一个(超级麻烦的)矩阵是存在的,见下面这个公式,其中(Rx,Ry,Rz)代表任意旋转轴:
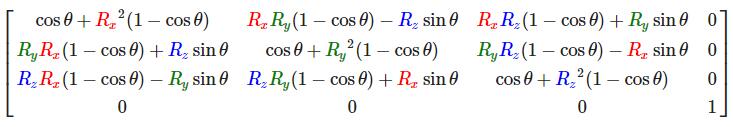
在数学上讨论如何生成这样的矩阵仍然超出了本节内容。但是记住,即使这样一个矩阵也不能完全解决万向节死锁问题(尽管会极大地避免)。避免万向节死锁的真正解决方案是使用四元数(Quaternion),它不仅更安全,而且计算会更有效率。
对四元数的理解会用到非常多的数学知识。如果你想了解四元数与3D旋转之间的关系,可以来阅读这篇的教程四元数与三维旋转。如果你对万向节死锁的概念仍不是那么清楚,可以来阅读教程的Bonus章节()。现在3Blue1Brown也已经开始了一个四元数的视频系列,他采用球极平面投影(Stereographic Projection)的方式将四元数投影到3D空间,同样有助于理解四元数的概念Visualizing quaternions。
矩阵的组合
使用矩阵进行变换的真正力量在于,根据矩阵之间的乘法,我们可以把多个变换组合到一个矩阵中。让我们看看我们是否能生成一个变换矩阵,让它组合多个变换。假设我们有一个顶点(x, y, z),我们希望将其缩放2倍,然后位移(1, 2, 3)个单位。我们需要一个位移和缩放矩阵来完成这些变换。结果的变换矩阵看起来像这样:

注意,当矩阵相乘时我们先写位移再写缩放变换的。矩阵乘法是不遵守交换律的,这意味着它们的顺序很重要。当矩阵相乘时,在最右边的矩阵是第一个与向量相乘的,所以你应该从右向左读这个乘法。建议您在组合矩阵时,先进行缩放操作,然后是旋转,最后才是位移,否则它们会(消极地)互相影响。比如,如果你先位移再缩放,位移的向量也会同样被缩放(译注:比如向某方向移动2米,2米也许会被缩放成1米)!
用最终的变换矩阵左乘我们的向量会得到以下结果:
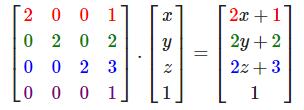
实践
OpenGL没有自带任何的矩阵和向量知识,所以我们必须定义自己的数学类和函数。在教程中我们更希望抽象所有的数学细节,使用已经做好了的数学库。幸运的是,有个易于使用,专门为OpenGL量身定做的数学库,那就是GLM。
GLM是OpenGL Mathematics的缩写,它是一个只有头文件的库,也就是说我们只需包含对应的头文件就行了,不用链接和编译。GLM可以在它们的网站上下载OpenGL Mathematics。把头文件的根目录复制到你的includes文件夹,然后你就可以使用这个库了。
PS:GLM库从0.9.9版本起,默认会将矩阵类型初始化为一个零矩阵(所有元素均为0),而不是单位矩阵(对角元素为1,其它元素为0)。如果你使用的是0.9.9或0.9.9以上的版本,你需要将所有的矩阵初始化改为 glm::mat4 mat = glm::mat4(1.0f)。如果你想与本教程的代码保持一致,请使用低于0.9.9版本的GLM,或者改用上述代码初始化所有的矩阵。
我们需要的GLM的大多数功能都可以从下面这3个头文件中找到:
1 |
我们来看看是否可以利用我们刚学的变换知识把一个向量(1, 0, 0)位移(1, 1, 0)个单位(注意,我们把它定义为一个glm::vec4类型的值,齐次坐标设定为1.0):
1 | glm::vec4 vec(1.0f, 0.0f, 0.0f, 1.0f); |
我们先用GLM内建的向量类定义一个叫做vec的向量。接下来定义一个mat4类型的trans,默认是一个4×4单位矩阵。下一步是创建一个变换矩阵,我们是把单位矩阵和一个位移向量传递给glm::translate函数来完成这个工作的(然后用给定的矩阵乘以位移矩阵就能获得最后需要的矩阵)。
之后我们把向量乘以位移矩阵并且输出最后的结果。如果你仍记得位移矩阵是如何工作的话,得到的向量应该是(1 + 1, 0 + 1, 0 + 0),也就是(2, 1, 0)。这个代码片段将会输出210,所以这个位移矩阵是正确的。
我们来做些更有意思的事情,让我们来旋转和缩放之前教程中的那个箱子。首先我们把箱子逆时针旋转90度。然后缩放0.5倍,使它变成原来的一半大。我们先来创建变换矩阵:
1 | glm::mat4 trans = glm::mat4(1.0f); |
首先,我们把箱子在每个轴都缩放到0.5倍,然后沿z轴旋转90度。GLM希望它的角度是弧度制的(Radian),所以我们使用glm::radians将角度转化为弧度。注意有纹理的那面矩形是在XY平面上的,所以我们需要把它绕着z轴旋转。因为我们把这个矩阵传递给了GLM的每个函数,GLM会自动将矩阵相乘,返回的结果是一个包括了多个变换的变换矩阵。
下一个大问题是:如何把矩阵传递给着色器?我们在前面简单提到过GLSL里也有一个mat4类型。所以我们将修改顶点着色器让其接收一个mat4的uniform变量,然后再用矩阵uniform乘以位置向量:
1 |
|
GLSL也有mat2和mat3类型,从而允许了像向量一样的混合运算。前面提到的所有数学运算(像是标量-矩阵相乘,矩阵-向量相乘和矩阵-矩阵相乘)在矩阵类型里都可以使用。当出现特殊的矩阵运算的时候我们会特别说明。
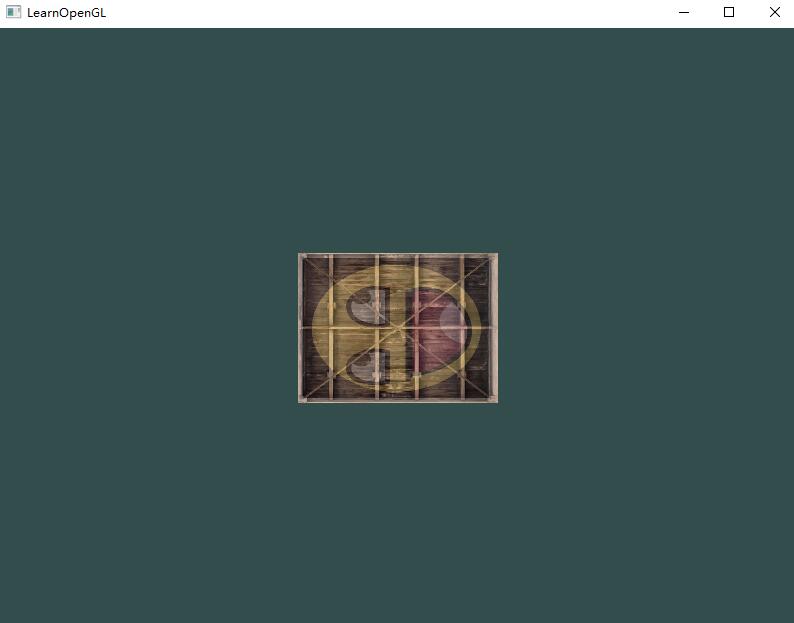
在把位置向量传给gl_Position之前,我们先添加一个uniform,并且将其与变换矩阵相乘。我们的箱子现在应该是原来的二分之一大小并(向左)旋转了90度。当然,我们仍需要把变换矩阵传递给着色器:
1 | unsigned int transformLoc = glGetUniformLocation(ourShader.ID, "transform"); |
我们首先查询uniform变量的地址,然后用有Matrix4fv后缀的glUniform函数把矩阵数据发送给着色器。第一个参数你现在应该很熟悉了,它是uniform的位置值。第二个参数告诉OpenGL我们将要发送多少个矩阵,这里是1。第三个参数询问我们我们是否希望对我们的矩阵进行置换(Transpose),也就是说交换我们矩阵的行和列。OpenGL开发者通常使用一种内部矩阵布局,叫做列主序(Column-major Ordering)布局。GLM的默认布局就是列主序,所以并不需要置换矩阵,我们填GL_FALSE。最后一个参数是真正的矩阵数据,但是GLM并不是把它们的矩阵储存为OpenGL所希望接受的那种,因此我们要先用GLM的自带的函数value_ptr来变换这些数据。
我们创建了一个变换矩阵,在顶点着色器中声明了一个uniform,并把矩阵发送给了着色器,着色器会变换我们的顶点坐标。最后的结果应该看起来像这样:
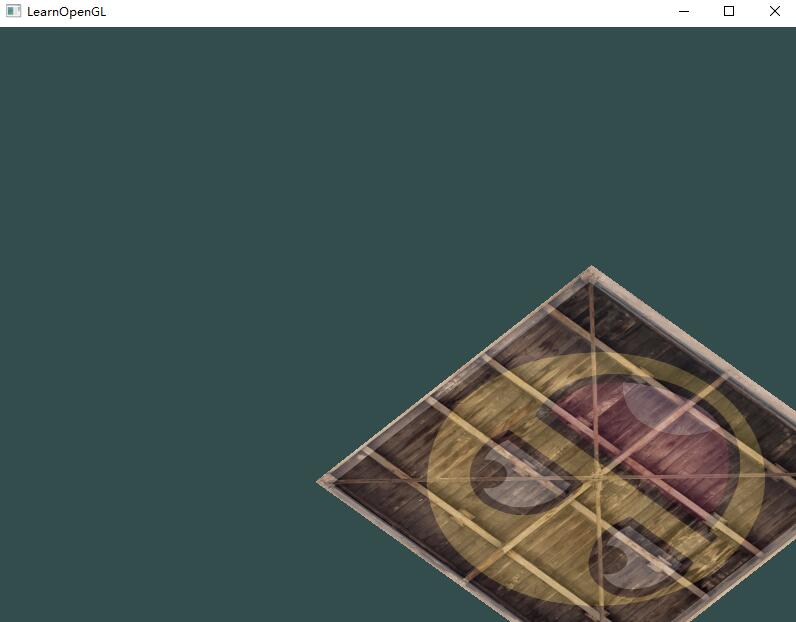
完美!我们的箱子向左侧旋转,并是原来的一半大小,所以变换成功了。我们现在做些更有意思的,看看我们是否可以让箱子随着时间旋转,我们还会重新把箱子放在窗口的右下角。要让箱子随着时间推移旋转,我们必须在游戏循环中更新变换矩阵,因为它在每一次渲染迭代中都要更新。我们使用GLFW的时间函数来获取不同时间的角度:
1 | glm::mat4 trans = glm::mat4(1.0f); |
要记住的是前面的例子中我们可以在任何地方声明变换矩阵,但是现在我们必须在每一次迭代中创建它,从而保证我们能够不断更新旋转角度。这也就意味着我们不得不在每次游戏循环的迭代中重新创建变换矩阵。通常在渲染场景的时候,我们也会有多个需要在每次渲染迭代中都用新值重新创建的变换矩阵。
在这里我们先把箱子围绕原点(0, 0, 0)旋转,之后,我们把旋转过后的箱子位移到屏幕的右下角。记住,实际的变换顺序应该与阅读顺序相反:尽管在代码中我们先位移再旋转,实际的变换却是先应用旋转再是位移的。
下一节中,我们会讨论怎样使用矩阵为顶点定义不同的坐标空间。这将是我们进入实时3D图像的第一步!
坐标系统
在上一个教程中,我们学习了如何有效地利用矩阵的变换来对所有顶点进行变换。OpenGL希望在每次顶点着色器运行后,我们可见的所有顶点都为标准化设备坐标(Normalized Device Coordinate, NDC)。也就是说,每个顶点的x,y,z坐标都应该在-1.0到1.0之间,超出这个坐标范围的顶点都将不可见。我们通常会自己设定一个坐标的范围,之后再在顶点着色器中将这些坐标变换为标准化设备坐标。然后将这些标准化设备坐标传入光栅器(Rasterizer),将它们变换为屏幕上的二维坐标或像素。
将坐标变换为标准化设备坐标,接着再转化为屏幕坐标的过程通常是分步进行的,也就是类似于流水线那样子。在流水线中,物体的顶点在最终转化为屏幕坐标之前还会被变换到多个坐标系统(Coordinate System)。将物体的坐标变换到几个过渡坐标系(Intermediate Coordinate System)的优点在于,在这些特定的坐标系统中,一些操作或运算更加方便和容易,这一点很快就会变得很明显。对我们来说比较重要的总共有5个不同的坐标系统:
- 局部空间(Local Space,或者称为物体空间(Object Space));
- 世界空间(World Space);
- 观察空间(View Space,或者称为视觉空间(Eye Space));
- 裁剪空间(Clip Space);
- 屏幕空间(Screen Space)。
这就是一个顶点在最终被转化为片段之前需要经历的所有不同状态。
概述
为了将坐标从一个坐标系变换到另一个坐标系,我们需要用到几个变换矩阵,最重要的几个分别是模型(Model)、观察(View)、投影(Projection)三个矩阵。
我们的顶点坐标起始于局部空间(Local Space),在这里它称为局部坐标(Local Coordinate),它在之后会变为世界坐标(World Coordinate),观察坐标(View Coordinate),裁剪坐标(Clip Coordinate),并最后以屏幕坐标(Screen Coordinate)的形式结束。下面的这张图展示了整个流程以及各个变换过程做了什么:
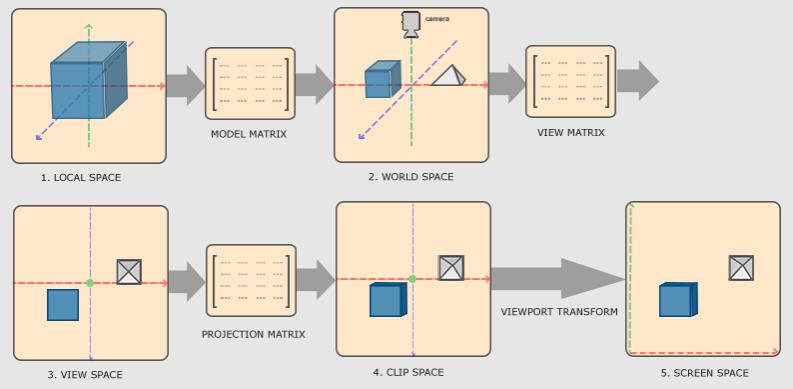
- 局部坐标是对象相对于局部原点的坐标,也是物体起始的坐标;
- 下一步是将局部坐标变换为世界空间坐标,世界空间坐标是处于一个更大的空间范围的。这些坐标相对于世界的全局原点,它们会和其它物体一起相对于世界的原点进行摆放;
- 接下来我们将世界坐标变换为观察空间坐标,使得每个坐标都是从摄像机或者说观察者的角度进行观察的;
- 坐标到达观察空间之后,我们需要将其投影到裁剪坐标。裁剪坐标会被处理至
-1.0到1.0的范围内,并判断哪些顶点将会出现在屏幕上(深度测试); - 最后,我们将裁剪坐标变换为屏幕坐标,我们将使用一个叫做视口变换(Viewport Transform)的过程。视口变换将位于
-1.0到1.0范围的坐标变换到由glViewport函数所定义的坐标范围内。最后变换出来的坐标将会送到光栅器,将其转化为片段。
我们之所以将顶点变换到各个不同的空间的原因是,有些操作在特定的坐标系统中才有意义且更方便。例如,当需要对物体进行修改的时候,在局部空间中来操作会更说得通;如果要对一个物体做出一个相对于其它物体位置的操作时,在世界坐标系中来做这个才更说得通,等等。
接下来我们将要更仔细地讨论各个坐标系统。
局部空间
局部空间是指物体所在的坐标空间,即对象最开始所在的地方。
模型的所有顶点都是在局部空间中:它们相对于你的物体来说都是局部的。
我们一直使用的那个箱子的顶点是被设定在-0.5到0.5的坐标范围中,(0, 0)是它的原点。这些都是局部坐标。
世界空间
如果我们将我们所有的物体导入到程序当中,它们有可能会全挤在世界的原点(0, 0, 0)上,这并不是我们想要的结果。我们想为每一个物体定义一个位置,从而能在更大的世界当中放置它们。世界空间中的坐标正如其名:是指顶点相对于世界的坐标。如果你希望将物体分散在世界上摆放(特别是非常真实的那样),这就是你希望物体变换到的空间。物体的坐标将会从局部变换到世界空间;该变换是由模型矩阵(Model Matrix)实现的。
模型矩阵是一种变换矩阵,它能通过对物体进行位移、缩放、旋转来将它置于它本应该在的位置或朝向。你可以将它想像为变换一个房子,你需要先将它缩小(它在局部空间中太大了),并将其位移至郊区的一个小镇,然后在y轴上往左旋转一点以搭配附近的房子。你也可以把上一节将箱子到处摆放在场景中用的那个矩阵大致看作一个模型矩阵;我们将箱子的局部坐标变换到场景/世界中的不同位置。
观察空间
观察空间经常被人们称之OpenGL的摄像机(Camera)(所以有时也称为摄像机空间(Camera Space)或视觉空间(Eye Space))。观察空间是将世界空间坐标转化为用户视野前方的坐标而产生的结果。因此观察空间就是从摄像机的视角所观察到的空间。而这通常是由一系列的位移和旋转的组合来完成,平移/旋转场景从而使得特定的对象被变换到摄像机的前方。这些组合在一起的变换通常存储在一个观察矩阵(View Matrix)里,它被用来将世界坐标变换到观察空间。在下一节中我们将深入讨论如何创建一个这样的观察矩阵来模拟一个摄像机。
裁剪空间
在一个顶点着色器运行的最后,OpenGL期望所有的坐标都能落在一个特定的范围内,且任何在这个范围之外的点都应该被裁剪掉(Clipped)。被裁剪掉的坐标就会被忽略,所以剩下的坐标就将变为屏幕上可见的片段。这也就是裁剪空间(Clip Space)名字的由来。
为了将顶点坐标从观察变换到裁剪空间,我们需要定义一个投影矩阵(Projection Matrix),它指定了一个范围的坐标,比如在每个维度上的-1000到1000。投影矩阵接着会将在这个指定的范围内的坐标变换为标准化设备坐标的范围(-1.0, 1.0)。所有在范围外的坐标不会被映射到在-1.0到1.0的范围之间,所以会被裁剪掉。在上面这个投影矩阵所指定的范围内,坐标(1250, 500, 750)将是不可见的,这是由于它的x坐标超出了范围,它被转化为一个大于1.0的标准化设备坐标,所以被裁剪掉了。
如果只是图元(Primitive),例如三角形,的一部分超出了裁剪体积(Clipping Volume),则OpenGL会重新构建这个三角形为一个或多个三角形让其能够适合这个裁剪范围。
由投影矩阵创建的观察箱(Viewing Box)被称为平截头体(Frustum),每个出现在平截头体范围内的坐标都会最终出现在用户的屏幕上。将特定范围内的坐标转化到标准化设备坐标系的过程(而且它很容易被映射到2D观察空间坐标)被称之为投影(Projection),因为使用投影矩阵能将3D坐标投影(Project)到很容易映射到2D的标准化设备坐标系中。
一旦所有顶点被变换到裁剪空间,最终的操作——透视除法(Perspective Division)将会执行,在这个过程中我们将位置向量的x,y,z分量分别除以向量的齐次w分量;透视除法是将4D裁剪空间坐标变换为3D标准化设备坐标的过程。这一步会在每一个顶点着色器运行的最后被自动执行。
在这一阶段之后,最终的坐标将会被映射到屏幕空间中(使用glViewport中的设定),并被变换成片段。
将观察坐标变换为裁剪坐标的投影矩阵可以为两种不同的形式,每种形式都定义了不同的平截头体。我们可以选择创建一个正射投影矩阵(Orthographic Projection Matrix)或一个透视投影矩阵(Perspective Projection Matrix)。
正射投影
正射投影矩阵定义了一个类似立方体的平截头箱,它定义了一个裁剪空间,在这空间之外的顶点都会被裁剪掉。创建一个正射投影矩阵需要指定可见平截头体的宽、高和长度。在使用正射投影矩阵变换至裁剪空间之后处于这个平截头体内的所有坐标将不会被裁剪掉。它的平截头体看起来像一个容器:
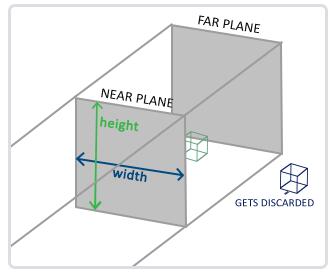
上面的平截头体定义了可见的坐标,它由由宽、高、近(Near)平面和远(Far)平面所指定。任何出现在近平面之前或远平面之后的坐标都会被裁剪掉。正射平截头体直接将平截头体内部的所有坐标映射为标准化设备坐标,因为每个向量的w分量都没有进行改变;如果w分量等于1.0,透视除法则不会改变这个坐标。
要创建一个正射投影矩阵,我们可以使用GLM的内置函数glm::ortho:
1 | glm::ortho(0.0f, 800.0f, 0.0f, 600.0f, 0.1f, 100.0f); |
前两个参数指定了平截头体的左右坐标,第三和第四参数指定了平截头体的底部和顶部。通过这四个参数我们定义了近平面和远平面的大小,然后第五和第六个参数则定义了近平面和远平面的距离。这个投影矩阵会将处于这些x,y,z值范围内的坐标变换为标准化设备坐标。
正射投影矩阵直接将坐标映射到2D平面中,即你的屏幕,但实际上一个直接的投影矩阵会产生不真实的结果,因为这个投影没有将透视(Perspective)考虑进去。所以我们需要透视投影矩阵来解决这个问题。
透视投影
如果你曾经体验过实际生活给你带来的景象,你就会注意到离你越远的东西看起来更小。这个奇怪的效果称之为透视(Perspective)。透视的效果在我们看一条无限长的高速公路或铁路时尤其明显,正如下面图片显示的那样:
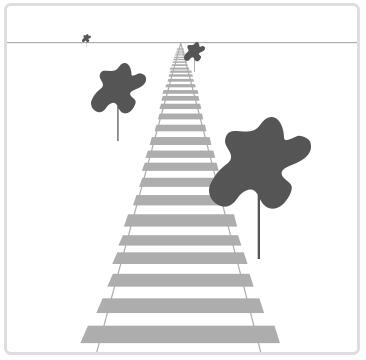
正如你看到的那样,由于透视,这两条线在很远的地方看起来会相交。这正是透视投影想要模仿的效果,它是使用透视投影矩阵来完成的。这个投影矩阵将给定的平截头体范围映射到裁剪空间,除此之外还修改了每个顶点坐标的w值,从而使得离观察者越远的顶点坐标w分量越大。被变换到裁剪空间的坐标都会在-w到w的范围之间(任何大于这个范围的坐标都会被裁剪掉)。OpenGL要求所有可见的坐标都落在-1.0到1.0范围内,作为顶点着色器最后的输出,因此,一旦坐标在裁剪空间内之后,透视除法就会被应用到裁剪空间坐标上:
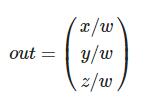
顶点坐标的每个分量都会除以它的w分量,距离观察者越远顶点坐标就会越小。这是也是w分量非常重要的另一个原因,它能够帮助我们进行透视投影。最后的结果坐标就是处于标准化设备空间中的。如果你对正射投影矩阵和透视投影矩阵是如何计算的很感兴趣(且不会对数学感到恐惧的话)我推荐这篇由Songho写的文章。
在GLM中可以这样创建一个透视投影矩阵:
1 | glm::perspective(glm::radians(45.0f), (float)width/(float)height, 0.1f, 100.0f); |
同样,glm::perspective所做的其实就是创建了一个定义了可视空间的大平截头体,任何在这个平截头体以外的东西最后都不会出现在裁剪空间体积内,并且将会受到裁剪。一个透视平截头体可以被看作一个不均匀形状的箱子,在这个箱子内部的每个坐标都会被映射到裁剪空间上的一个点。下面是一张透视平截头体的图片:
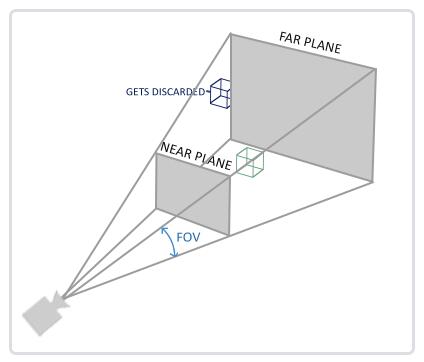
glm::perspective的第一个参数定义了fov的值,它表示的是视野(Field of View),并且设置了观察空间的大小。如果想要一个真实的观察效果,它的值通常设置为45.0f,但想要一个末日风格的结果你可以将其设置一个更大的值。第二个参数设置了宽高比,由视口的宽除以高所得。第三和第四个参数设置了平截头体的近和远平面。我们通常设置近距离为0.1f,而远距离设为100.0f。所有在近平面和远平面内且处于平截头体内的顶点都会被渲染。
当你把透视矩阵的 near 值设置太大时(如10.0f),OpenGL会将靠近摄像机的坐标(在0.0f和10.0f之间)都裁剪掉,这会导致一个你在游戏中很熟悉的视觉效果:在太过靠近一个物体的时候你的视线会直接穿过去。
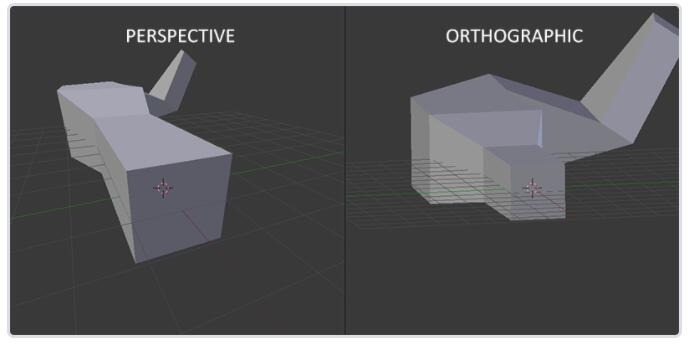
当使用正射投影时,每一个顶点坐标都会直接映射到裁剪空间中而不经过任何精细的透视除法(它仍然会进行透视除法,只是w分量没有被改变(它保持为1),因此没有起作用)。因为正射投影没有使用透视,远处的物体不会显得更小,所以产生奇怪的视觉效果。由于这个原因,正射投影主要用于二维渲染以及一些建筑或工程的程序,在这些场景中我们更希望顶点不会被透视所干扰。某些如 Blender 等进行三维建模的软件有时在建模时也会使用正射投影,因为它在各个维度下都更准确地描绘了每个物体。下面你能够看到在Blender里面使用两种投影方式的对比:
把它们都组合到一起
我们为上述的每一个步骤都创建了一个变换矩阵:模型矩阵、观察矩阵和投影矩阵。一个顶点坐标将会根据以下过程被变换到裁剪坐标:
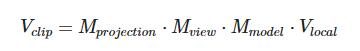
注意矩阵运算的顺序是相反的(记住我们需要从右往左阅读矩阵的乘法)。最后的顶点应该被赋值到顶点着色器中的gl_Position,OpenGL将会自动进行透视除法和裁剪。
然后呢?顶点着色器的输出要求所有的顶点都在裁剪空间内,这正是我们刚才使用变换矩阵所做的。OpenGL然后对裁剪坐标执行透视除法从而将它们变换到标准化设备坐标。OpenGL会使用glViewPort内部的参数来将标准化设备坐标映射到屏幕坐标,每个坐标都关联了一个屏幕上的点(在我们的例子中是一个800x600的屏幕)。这个过程称为视口变换。
进入3D
既然我们知道了如何将3D坐标变换为2D坐标,我们可以开始使用真正的3D物体,而不是枯燥的2D平面了。
在开始进行3D绘图时,我们首先创建一个模型矩阵。这个模型矩阵包含了位移、缩放与旋转操作,它们会被应用到所有物体的顶点上,以变换它们到全局的世界空间。让我们变换一下我们的平面,将其绕着x轴旋转,使它看起来像放在地上一样。这个模型矩阵看起来是这样的:
1 | glm::mat4 model = glm::mat4(1.0f); |
通过将顶点坐标乘以这个模型矩阵,我们将该顶点坐标变换到世界坐标。我们的平面看起来就是在地板上,代表全局世界里的平面。
接下来我们需要创建一个观察矩阵。我们想要在场景里面稍微往后移动,以使得物体变成可见的(当在世界空间时,我们位于原点(0,0,0))。要想在场景里面移动,先仔细想一想下面这个句子:
- 将摄像机向后移动,和将整个场景向前移动是一样的。
这正是观察矩阵所做的,我们以相反于摄像机移动的方向移动整个场景。因为我们想要往后移动,并且OpenGL是一个右手坐标系(Right-handed System),所以我们(摄像机)需要沿着z轴的正方向移动。我们会通过将场景沿着z轴负方向平移来实现。它会给我们一种我们在往后移动的感觉。
右手坐标系(Right-handed System):按照惯例,OpenGL是一个右手坐标系。简单来说,就是正x轴在你的右手边,正y轴朝上,而正z轴是朝向后方的。想象你的屏幕处于三个轴的中心,则正z轴穿过你的屏幕朝向你。坐标系画起来如下:
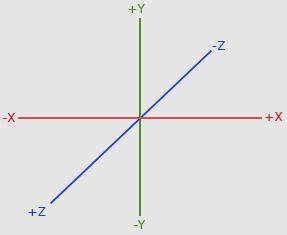
为了理解为什么被称为右手坐标系,按如下的步骤做:
- 沿着正y轴方向伸出你的右臂,手指着上方;
- 大拇指指向右方;
- 食指指向上方;
- 中指向下弯曲90度。
如果你的动作正确,那么你的大拇指指向正x轴方向,食指指向正y轴方向,中指指向正z轴方向。如果你用左臂来做这些动作,你会发现z轴的方向是相反的。这个叫做左手坐标系,它被DirectX广泛地使用。注意在标准化设备坐标系中OpenGL实际上使用的是左手坐标系(投影矩阵交换了左右手)。
就目前来说,观察矩阵是这样的:
1 | glm::mat4 view = glm::mat4(1.0f); |
最后我们需要做的是定义一个投影矩阵。我们希望在场景中使用透视投影,所以像这样声明一个投影矩阵:
1 | glm::mat4 projection = glm::mat4(1.0f); |
既然我们已经创建了变换矩阵,我们应该将它们传入顶点着色器。首先,让我们在顶点着色器中声明一个uniform变换矩阵然后将它乘以顶点坐标:
1 |
|
我们还应该将矩阵传入顶点着色器(这通常在每次的渲染迭代中进行,因为变换矩阵会经常变动):
1 | int modelLoc = glGetUniformLocation(ourShader.ID, "model"); |
我们的顶点坐标已经使用模型、观察和投影矩阵进行变换了,最终的物体应该会:
- 稍微向后倾斜至地板方向;
- 离我们有一些距离;
- 有透视效果(顶点越远,变得越小)。
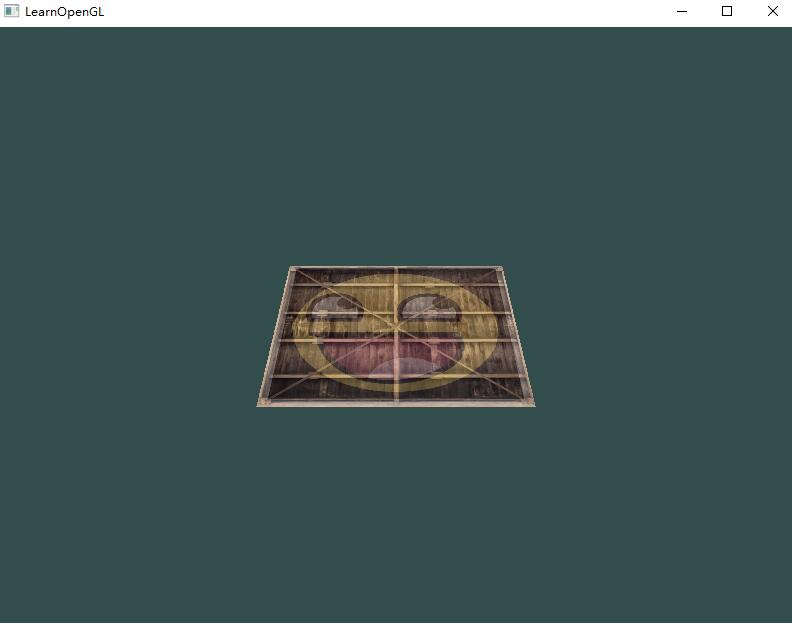
更多的3D
到目前为止,我们一直都在使用一个2D平面,而且甚至是在3D空间里!所以,让我们大胆地拓展我们的2D平面为一个3D立方体。要想渲染一个立方体,我们一共需要36个顶点(6个面 x 每个面有2个三角形组成 x 每个三角形有3个顶点)。
1 | float vertices[] = { |
为了有趣一点,我们将让立方体随着时间旋转:
1 | model = glm::rotate(model, (float)glfwGetTime() * glm::radians(50.0f), glm::vec3(0.5f, 1.0f, 0.0f)); |
然后我们使用glDrawArrays来绘制立方体,但这一次总共有36个顶点:
1 | glDrawArrays(GL_TRIANGLES, 0, 36); |

这的确有点像是一个立方体,但又有种说不出的奇怪。立方体的某些本应被遮挡住的面被绘制在了这个立方体其他面之上。之所以这样是因为OpenGL是一个三角形一个三角形地来绘制你的立方体的,所以即便之前那里有东西它也会覆盖之前的像素。因为这个原因,有些三角形会被绘制在其它三角形上面,虽然它们本不应该是被覆盖的。
幸运的是,OpenGL存储深度信息在一个叫做Z缓冲(Z-buffer)的缓冲中,它允许OpenGL决定何时覆盖一个像素而何时不覆盖。通过使用Z缓冲,我们可以配置OpenGL来进行深度测试。
Z缓冲
OpenGL存储它的所有深度信息于一个Z缓冲(Z-buffer)中,也被称为深度缓冲(Depth Buffer)。GLFW会自动为你生成这样一个缓冲(就像它也有一个颜色缓冲来存储输出图像的颜色)。深度值存储在每个片段里面(作为片段的z值),当片段想要输出它的颜色时,OpenGL会将它的深度值和z缓冲进行比较,如果当前的片段在其它片段之后,它将会被丢弃,否则将会覆盖。这个过程称为深度测试(Depth Testing),它是由OpenGL自动完成的。
然而,如果我们想要确定OpenGL真的执行了深度测试,首先我们要告诉OpenGL我们想要启用深度测试,它默认是关闭的。我们可以通过glEnable函数来开启深度测试。glEnable和glDisable函数允许我们启用或禁用某个OpenGL功能。这个功能会一直保持启用/禁用状态,直到另一个调用来禁用/启用它。现在我们想启用深度测试,需要开启GL_DEPTH_TEST:
1 | glEnable(GL_DEPTH_TEST); |
因为我们使用了深度测试,我们也想要在每次渲染迭代之前清除深度缓冲(否则前一帧的深度信息仍然保存在缓冲中)。就像清除颜色缓冲一样,我们可以通过在glClear函数中指定DEPTH_BUFFER_BIT位来清除深度缓冲:
1 | glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT); |

更多的立方体!
现在我们想在屏幕上显示10个立方体。每个立方体看起来都是一样的,区别在于它们在世界的位置及旋转角度不同。立方体的图形布局已经定义好了,所以当渲染更多物体的时候我们不需要改变我们的缓冲数组和属性数组,我们唯一需要做的只是改变每个对象的模型矩阵来将立方体变换到世界坐标系中。
首先,让我们为每个立方体定义一个位移向量来指定它在世界空间的位置。我们将在一个glm::vec3数组中定义10个立方体位置:
1 | glm::vec3 cubePositions[] = { |
现在,在游戏循环中,我们调用glDrawArrays 10次,但这次在我们渲染之前每次传入一个不同的模型矩阵到顶点着色器中。我们将会在游戏循环中创建一个小的循环用不同的模型矩阵渲染我们的物体10次。注意我们也对每个箱子加了一点旋转:
1 | glBindVertexArray(VAO); |

练习题
- 对GLM的projection函数中的FoV和aspect-ratio参数进行实验。看能否搞懂它们是如何影响透视平截头体的;
- 将观察矩阵在各个方向上进行位移,来看看场景是如何改变的。注意把观察矩阵当成摄像机对象;
- 使用模型矩阵只让是3倍数的箱子旋转(以及第1个箱子),而让剩下的箱子保持静止。
摄像机
前面的教程中我们讨论了观察矩阵以及如何使用观察矩阵移动场景(我们向后移动了一点)。OpenGL本身没有摄像机(Camera)的概念,但我们可以通过把场景中的所有物体往相反方向移动的方式来模拟出摄像机,产生一种我们在移动的感觉,而不是场景在移动。
本节我们将会讨论如何在OpenGL中配置一个摄像机,并且将会讨论FPS风格的摄像机,让你能够在3D场景中自由移动。我们也会讨论键盘和鼠标输入,最终完成一个自定义的摄像机类。
摄像机/观察空间
当我们讨论摄像机/观察空间(Camera/View Space)的时候,是在讨论以摄像机的视角作为场景原点时场景中所有的顶点坐标:观察矩阵把所有的世界坐标变换为相对于摄像机位置与方向的观察坐标。要定义一个摄像机,我们需要它在世界空间中的位置、观察的方向、一个指向它右侧的向量以及一个指向它上方的向量。细心的读者可能已经注意到我们实际上创建了一个三个单位轴相互垂直的、以摄像机的位置为原点的坐标系。
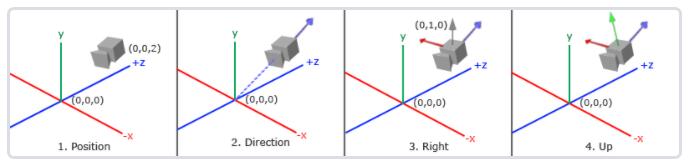
- 摄像机位置
获取摄像机位置很简单。摄像机位置简单来说就是世界空间中一个指向摄像机位置的向量。我们把摄像机位置设置为上一节中的那个相同的位置:
1 | glm::vec3 cameraPos = glm::vec3(0.0f, 0.0f, 3.0f); |
- 摄像机方向
下一个需要的向量是摄像机的方向,这里指的是摄像机指向哪个方向。现在我们让摄像机指向场景原点:``(0, 0, 0)。还记得如果将两个矢量相减,我们就能得到这两个矢量的差吗?用场景原点向量减去摄像机位置向量的结果就是摄像机的指向向量。由于我们知道摄像机指向z轴负方向,但我们希望方向向量(Direction Vector)指向摄像机的z轴正方向。如果我们交换相减的顺序,我们就会获得一个指向摄像机正z轴方向的向量:
1 | glm::vec3 cameraTarget = glm::vec3(0.0f, 0.0f, 0.0f); |
方向向量(Direction Vector)并不是最好的名字,因为它实际上指向从它到目标向量的相反方向(译注:注意看前面的那个图,蓝色的方向向量大概指向z轴的正方向,与摄像机实际指向的方向是正好相反的)。
- 右轴
我们需要的另一个向量是一个右向量(Right Vector),它代表摄像机空间的x轴的正方向。为获取右向量我们需要先使用一个小技巧:先定义一个上向量(Up Vector)。接下来把上向量和第二步得到的方向向量进行叉乘。两个向量叉乘的结果会同时垂直于两向量,因此我们会得到指向x轴正方向的那个向量(如果我们交换两个向量叉乘的顺序就会得到相反的指向x轴负方向的向量):
1 | glm::vec3 up = glm::vec3(0.0f, 1.0f, 0.0f); |
- 上轴
现在我们已经有了x轴向量和z轴向量,获取一个指向摄像机的正y轴向量就相对简单了:我们把方向向量和右向量进行叉乘:
1 | // 注意叉乘顺序,右手系 |
对于想学到更多数学原理的读者,提示一下,在线性代数中这个处理叫做格拉姆—施密特正交化(Gram-Schmidt Process)。使用这些摄像机向量我们就可以创建一个LookAt矩阵了,它在创建摄像机的时候非常有用。
Look At
使用矩阵的好处之一是如果你使用3个相互垂直(或非线性)的轴定义了一个坐标空间,你可以用这3个轴外加一个平移向量来创建一个矩阵,并且你可以用这个矩阵乘以任何向量来将其变换到那个坐标空间。这正是LookAt矩阵所做的,现在我们有了3个相互垂直的轴和一个定义摄像机空间的位置坐标,我们可以创建我们自己的LookAt矩阵了:
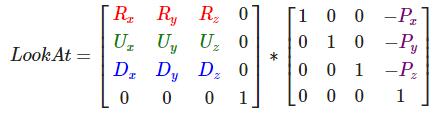
其中R是右向量,U是上向量,D是方向向量,P是摄像机位置向量。注意,位置向量是相反的,因为我们最终希望把世界平移到与我们自身移动的相反方向。把这个LookAt矩阵作为观察矩阵可以很高效地把所有世界坐标变换到刚刚定义的观察空间。LookAt矩阵就像它的名字表达的那样:它会创建一个看着(Look at)给定目标的观察矩阵。
幸运的是,GLM已经提供了这些支持。我们要做的只是定义一个摄像机位置,一个目标位置和一个表示世界空间中的上向量的向量(我们计算右向量使用的那个上向量)。接着GLM就会创建一个LookAt矩阵,我们可以把它当作我们的观察矩阵:
1 | glm::mat4 view = glm::mat4(1.0f); |
glm::LookAt函数需要一个位置、目标和上向量。它会创建一个和在上一节使用的一样的观察矩阵。
在讨论用户输入之前,我们先来做些有意思的事,把我们的摄像机在场景中旋转。我们会将摄像机的注视点保持在(0, 0, 0)。
1 | float radius = 10.f; |

自由移动
1 | glm::vec3 cameraPos = glm::vec3(0.0f, 0.0f, 3.0f); |
注意,我们对右向量进行了标准化。如果我们没对这个向量进行标准化,最后的叉乘结果会根据cameraFront变量返回大小不同的向量。如果我们不对向量进行标准化,我们就得根据摄像机的朝向不同加速或减速移动了,但如果进行了标准化移动就是匀速的。
LookAt函数现在成了:
1 | glm::mat4 view = glm::lookAt(cameraPos, cameraPos + cameraFront, cameraUp); |
我们已经为GLFW的键盘输入定义过一个process_input函数了,我们来新添加几个需要检查的按键命令:
1 | float cameraSpeed = 0.05f; // adjust accordingly |

移动速度
目前我们的移动速度是个常量。理论上没什么问题,但是实际情况下根据处理器的能力不同,有些人可能会比其他人每秒绘制更多帧,也就是以更高的频率调用process_input函数。结果就是,根据配置的不同,有些人可能移动很快,而有些人会移动很慢。当你发布你的程序的时候,你必须确保它在所有硬件上移动速度都一样。
图形程序和游戏通常会跟踪一个时间差(Deltatime)变量,它储存了渲染上一帧所用的时间。我们把所有速度都去乘以deltaTime值。结果就是,如果我们的deltaTime很大,就意味着上一帧的渲染花费了更多时间,所以这一帧的速度需要变得更高来平衡渲染所花去的时间。使用这种方法时,无论你的电脑快还是慢,摄像机的速度都会相应平衡,这样每个用户的体验就都一样了。
我们跟踪两个全局变量来计算出deltaTime值:
1 | float deltaTime = 0.0f; // 当前帧与上一帧的时间差 |
在每一帧中我们计算出新的deltaTime以备后用。
1 | float currentFrame = glfwGetTime(); |
现在我们有了deltaTime,在计算速度的时候可以将其考虑进去了:
1 | float cameraSpeed = 2.5f * deltaTime; |

现在我们有了一个在任何系统上移动速度都一样的摄像机(近似一样)。
视角移动
现在还不能转向,移动很受限制,是时候加入鼠标了!
为了能够改变视角,我们需要根据鼠标的输入来该表cameraFront向量,然而,根据鼠标移动改变方向向量有点复杂,需要一些三角学知识。
欧拉角
欧拉角(Euler Angle)是可以表示3D空间中任何旋转的3个值,由莱昂哈德·欧拉(Leonhard Euler)在18世纪提出。一共有3种欧拉角:俯仰角(Pitch)、偏航角(Yaw)和滚转角(Roll),下面的图片展示了它们的含义:
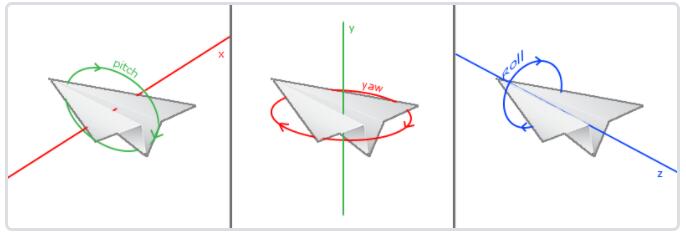
俯仰角是描述我们如何往上或往下看的角,可以在第一张图中看到。第二张图展示了偏航角,偏航角表示我们往左和往右看的程度。滚转角代表我们如何翻滚摄像机,通常在太空飞船的摄像机中使用。每个欧拉角都有一个值来表示,把三个角结合起来我们就能够计算3D空间中任何的旋转向量了。
对于我们的摄像机系统来说,我们只关心俯仰角和偏航角,所以我们不会讨论滚转角。给定一个俯仰角和偏航角,我们可以把它们转换为一个代表新的方向向量的3D向量。俯仰角和偏航角转换为方向向量的处理需要一些三角学知识,我们先从最基本的情况开始:
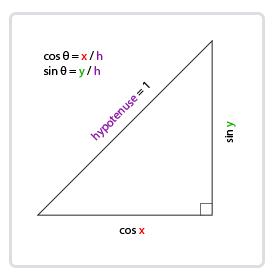
如果我们把斜边边长定义为1,我们就能知道邻边的长度是cos(x/h)=cos(x/1)=cosx,它的对边是sin(y/h)=sin(y/1)=siny。这样我们获得了能够得到x和y方向长度的通用公式,它们取决于所给的角度。我们使用它来计算方向向量的分量:
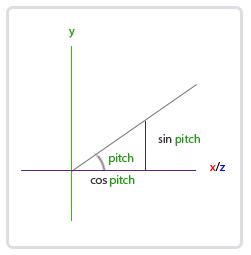
这个三角形看起来和前面的三角形很像,所以如果我们想象自己在xz平面上,看向y轴,我们可以基于第一个三角形计算来计算它的长度/y方向的强度(Strength)(我们往上或往下看多少)。从图中我们可以看到对于一个给定俯仰角的y值等于sinθ:
1 | direction.y = sin(glm::radians(pitch)); // 注意我们先把角度转为弧度 |
这里我们只更新了y值,仔细观察x和z分量也被影响了。从三角形中我们可以看到它们的值等于:
1 | direction.x = cos(glm::radians(pitch)); |
看看我们是否能够为偏航角找到需要的分量:
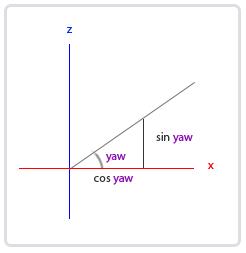
就像俯仰角的三角形一样,我们可以看到x分量取决于cos(yaw)的值,z值同样取决于偏航角的正弦值。把这个加到前面的值中,会得到基于俯仰角和偏航角的方向向量:
1 | direction.x = cos(glm::radians(pitch)) * cos(glm::radians(yaw)); |
这样我们就有了一个可以把俯仰角和偏航角转化为用来自由旋转视角的摄像机的3维方向向量了。你可能会奇怪:我们怎么得到俯仰角和偏航角?
鼠标输入
偏航角和俯仰角是通过鼠标(或手柄)移动获得的,水平的移动影响偏航角,竖直的移动影响俯仰角。它的原理就是,储存上一帧鼠标的位置,在当前帧中我们当前计算鼠标位置与上一帧的位置相差多少。如果水平/竖直差别越大那么俯仰角或偏航角就改变越大,也就是摄像机需要移动更多的距离。
首先我们要告诉GLFW,它应该隐藏光标,并捕捉(Capture)它。捕捉光标表示的是,如果焦点在你的程序上(译注:即表示你正在操作这个程序,Windows中拥有焦点的程序标题栏通常是有颜色的那个,而失去焦点的程序标题栏则是灰色的),光标应该停留在窗口中(除非程序失去焦点或者退出)。我们可以用一个简单地配置调用来完成:
1 | glfwSetInputMode(window, GLFW_CURSOR, GLFW_CURSOR_DISABLED); |
在调用这个函数之后,无论我们怎么去移动鼠标,光标都不会显示了,它也不会离开窗口(避免移出窗口就不能再旋转摄像机了)。对于FPS摄像机系统来说非常完美。
为了计算俯仰角和偏航角,我们需要让GLFW监听鼠标移动事件。(和键盘输入相似)我们会用一个回调函数来完成,函数的原型如下:
1 | void mouse_callback(GLFWwindow* window, double xpos, double ypos); |
这里的xpos和ypos代表当前鼠标的位置。当我们用GLFW注册了回调函数之后,鼠标一移动mouse_callback函数就会被调用:
1 | glfwSetCursorPosCallback(window, mouse_callback); |
在处理FPS风格摄像机的鼠标输入的时候,我们必须在最终获取方向向量之前做下面这几步:
- 计算鼠标距上一帧的偏移量;
- 把偏移量添加到摄像机的俯仰角和偏航角中;
- 对偏航角和俯仰角进行最大和最小值的限制(视野限制);
- 计算方向向量。
第一步是计算鼠标自上一帧的偏移量。我们必须先在程序中储存上一帧的鼠标位置,我们把它的初始值设置为屏幕的中心(屏幕的尺寸是800x600):
1 | float lastX = 400, lastY = 300; |
然后在鼠标的回调函数中我们计算当前帧和上一帧鼠标位置的偏移量:
1 | float xoffset = xpos - lastX; |
注意我们把偏移量乘以了sensitivity(灵敏度)值。如果我们忽略这个值,鼠标移动就会太大了;你可以自己实验一下,找到适合自己的灵敏度值。
接下来我们把偏移量加到全局变量pitch和yaw上:
1 | yaw += xoffset; |
第三步,我们需要给摄像机添加一些限制,这样摄像机就不会发生奇怪的移动了(这样也会避免一些奇怪的问题)。对于俯仰角,要让用户不能看向高于89度的地方(在90度时视角会发生逆转,所以我们把89度作为极限),同样也不允许小于-89度。这样能够保证用户只能看到天空或脚下,但是不能超越这个限制。我们可以在值超过限制的时候将其改为极限值来实现:
1 | if(pitch > 89.0f) |
注意我们没有给偏航角设置限制,这是因为我们不希望限制用户的水平旋转。当然,给偏航角设置限制也很容易,如果你愿意可以自己实现。
第四也是最后一步,就是通过俯仰角和偏航角来计算以得到真正的方向向量:
1 | glm::vec3 front; |
计算出来的方向向量就会包含根据鼠标移动计算出来的所有旋转了。由于cameraFront向量已经包含在GLM的lookAt函数中,我们这就没什么问题了。

如果你现在运行代码,你会发现在窗口第一次获取焦点的时候摄像机会突然跳一下。这个问题产生的原因是,在你的鼠标移动进窗口的那一刻,鼠标回调函数就会被调用,这时候的xpos和ypos会等于鼠标刚刚进入屏幕的那个位置。这通常是一个距离屏幕中心很远的地方,因而产生一个很大的偏移量,所以就会跳了。我们可以简单的使用一个bool变量检验我们是否是第一次获取鼠标输入,如果是,那么我们先把鼠标的初始位置更新为xpos和ypos值,这样就能解决这个问题;接下来的鼠标移动就会使用刚进入的鼠标位置坐标来计算偏移量了:
1 | // 这个bool变量初始时是设定为true的 |
最后mouse_callback的代码应该是这样的:
1 | void mouse_callback(GLFWwindow* window, double xpos, double ypos) { |
计算cameraFront这部分放在mouse_callback中可能更适合一点,因为它只有在鼠标移动的时候才会发生改变,如果放在渲染循环中,计算可能是比较冗余的,因为其实有可能在几个帧中间鼠标并没有发生移动,所以没有必要去计算。
缩放
作为我们摄像机系统的一个附加内容,我们还会来实现一个缩放(Zoom)接口。在之前的教程中我们说视野(Field of View)或fov定义了我们可以看到场景中多大的范围。当视野变小时,场景投影出来的空间就会减小,产生放大(Zoom In)了的感觉。我们会使用鼠标的滚轮来放大和缩小。与鼠标移动、键盘输入一样,我们需要一个鼠标滚轮的回调函数:
1 | void scroll_callback(GLFWwindow* window, double xoffset, double yoffset) |
当滚动鼠标滚轮的时候,yoffset值代表我们竖直滚动的大小。当scroll_callback函数被调用后,我们改变全局变量fov变量的内容。因为45.0f是默认的视野值,我们将会把缩放级别(Zoom Level)限制在1.0f到45.0f。
我们现在在每一帧都必须把透视投影矩阵上传到GPU,但现在使用fov变量作为它的视野:
1 | projection = glm::perspective(glm::radians(fov), 800.0f / 600.0f, 0.1f, 100.0f); |
最后不要忘记注册鼠标滚轮的回调函数:
1 | glfwSetScrollCallback(window, scroll_callback); |
现在,我们就实现了一个简单的摄像机系统了,它能够让我们在3D环境中自由移动。
注意,使用欧拉角的摄像机系统并不完美。根据你的视角限制或者是配置,你仍然可能引入万向节死锁问题。最好的摄像机系统是使用四元数(Quaternions)的,但我们将会把这个留到后面讨论。
摄像机类
接下来的教程中,我们将会一直使用一个摄像机来浏览场景,从各个角度观察结果。然而,由于一个摄像机会占用每篇教程很大的篇幅,我们将会从细节抽象出来,创建我们自己的摄像机对象,它会完成大多数的工作,而且还会提供一些附加的功能。与着色器教程不同,我们不会带你一步一步创建摄像机类,我们只会提供你一份(有完整注释的)代码,如果你想知道它的内部构造的话可以自己去阅读。
和着色器对象一样,我们把摄像机类写在一个单独的头文件中。
1 |
我们介绍的摄像机系统是一个FPS风格的摄像机,它能够满足大多数情况需要,而且与欧拉角兼容,但是在创建不同的摄像机系统,比如飞行模拟摄像机,时就要当心。每个摄像机系统都有自己的优点和不足,所以确保对它们进行了详细研究。比如,这个FPS摄像机不允许俯仰角大于90度,而且我们使用了一个固定的上向量(0, 1, 0),这在需要考虑滚转角的时候就不能用了。
词汇复习
- OpenGL:一个定义了函数布局和输出的图形API的正式规范;
- GLAD:一个拓展加载库,用来为我们加载并设定所有OpenGL函数指针,从而让我们能够使用所有(现代)OpenGL函数;
- 视口(Viewport):我们需要渲染的窗口;
- 图形管线(Graphics Pipeline):一个顶点在呈现为像素之前经过的全部过程;
- 着色器(Shader):一个运行在显卡上的小型程序,很多阶段的图形管道都可以使用自定义的着色器来代替原有的功能,在OpenGL有些部分是我们必须提供的;
- 标准化设备坐标(Normalized Device Coordinates, NDC):顶点在通过在剪裁坐标系中剪裁与透视除法后最终呈现在的坐标系。所有位置在NDC下-1.0到1.0的顶点将不会被丢弃并且可见;
- VBO-顶点缓冲对象(Vertex Buffer Object):一个调用显存并存储所有顶点数据供显卡使用的缓冲对象;
- VAO-顶点数组对象(Vertex Array Object):存储缓冲区和顶点属性状态;
- EBO-索引缓冲对象(Element Buffer Object):一个存储索引供索引化绘制使用的缓冲对象;
- Uniform:一个特殊类型的GLSL变量。它是全局的(在一个着色器程序中每一个着色器都能够访问uniform变量),并且只需要被设定一次;
- 纹理(Texture):一种包裹着物体的特殊类型图像,给物体精细的视觉效果;
- 纹理缠绕(Texture Wrapping):定义了一种当纹理顶点超出范围(0, 1)时指定OpenGL如何采样纹理的模式;
- 纹理过滤(Texture Filtering):定义了一种当有多种纹素选择时指定OpenGL如何采样纹理的模式。这通常在纹理被放大情况下发生;
- 多级渐远纹理(Mipmaps):被存储的材质的一些缩小版本,根据距观察者的距离会使用材质的合适大小;
- stb_image.h:图像加载库;
- 纹理单元(Texture Units):通过绑定纹理到不同纹理单元从而允许多个纹理在同一对象上渲染;
- 向量(Vector):一个定义了在空间中方向和/或位置的数学实体;
- 矩阵(Matrix):一个矩形阵列的数学表达式;
- GLM:一个为OpenGL打造的数学库;
- 局部空间(Local Space):一个物体的初始空间。所有的坐标都是相对于物体的原点的;
- 世界空间(World Space):所有的坐标都相对于全局原点;
- 观察空间(View Space):所有的坐标都是从摄像机的视角观察的;
- 裁剪空间(Clip Space):所有的坐标都是从摄像机视角观察的,但是该空间应用了投影。这个空间应该是一个顶点坐标最终的空间,作为顶点着色器的输出。OpenGL负责处理剩下的事情(裁剪/透视除法);
- 屏幕空间(Screen Space):所有的坐标都由屏幕视角来观察。坐标的范围是从0到屏幕的宽/高;
- LookAt矩阵:一种特殊类型的观察矩阵,它创建了一个坐标系,其中所有坐标都根据从一个位置正在观察目标的用户旋转或者平移;
- 欧拉角(Euler Angles):被定义为偏航角(Yaw),俯仰角(Pitch),和滚转角(Roll)从而允许我们通过这三个值构造任何3D方向。
《LearnOpenGL》入门 笔记

