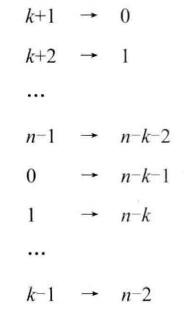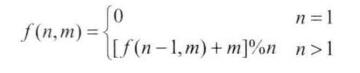沟通和学习能力是面试中关键的考查点。
1 面试官谈能力 大佬们说的名言名句。
咕咕待更。
2 沟通能力和学习能力 沟通能力 随着软件、系统功能越来越复杂,开发团队的规模也随之扩张,开发者、测试者和项目经理之间的沟通交流也变得越来越重要。也正因如此,很多公司在面试的时候都会注意考查应聘者的沟通能力。这邀请应聘者无论是在介绍项目经验 还是在介绍解题思路 的时候,都需要逻辑清晰明了 ,语言详略得当 ,表述的时候重点突出、观点明确 。
学习能力 计算机是一门更新速度很快的学科,每年都有新的技术不断涌现。因此,作为从业人员需要具备很强的学习能力 ,否则时间一长就会跟不上技术进步的步伐,也正是因为这个原因,IT公司在面试的时候,都会重视考查应聘者的学习能力。只有具备很强的学习能力及学习愿望的人,才能不断完善自己的知识结构,不断学习新的先进技术 ,让自己的职业生涯保持长久的生命力。
通常面试官有两种方法考查应聘者的学习能力 。第一种方法 是询问应聘者最近在看什么书或者在做什么项目、从中学到了哪些新技术 。面试官可以用这个问题了解应聘者的学习愿望和学习能力。第二种方法是抛出一个新概念 ,接下来观察应聘者能不能在短时间内理解这个新概念并解决相关的问题。当面试官提出新概念时,他期待应聘者能够通过思考、提问、再思考的过程,理解它们并最终解决问题 。
善于学习、沟通的人也善于提问 面试官提出一个新概念,应聘者没有听说过它,于是他在已有的理解基础上提出进一步地问题,在得到面试官答复之后,思考再提问,几个来回之后掌握了这个概念。这个过程就能体现应聘者的学习能力。建议应聘者在面试过程中遇到不明白的地方多提问,这样可以表现自己态度积极、求知欲望强烈(但是一些行业领域基础的东西不知道还是蛮尴尬的hhh)。
有些面试官故意一开始不把题目描述清楚,让题目存在一定的二义性,他期待应聘者可以一步步通过提问来弄明白题目的要求,这也是在考查应聘者的沟通能力(因为实际工作中也是这样的)。
3 知识迁移能力 所谓学习能力,很重要的一点就是根据已经掌握的知识、技术,能够迅速学习、理解新的技术并运用到实际工作中去 。大部分新的技术都不是凭空产生的,而是在已有技术的基础上发展起来的。这就要求我们能够把对已有技术的理解迁移到学习新技术的过程中去,也就是要具备很强的知识迁移能力。
面试官考查应聘者知识迁移能力的一种方法是把经典的问题稍作变换 。这时候面试官期待应聘者能够找到和经典问题的联系,并从中受到启发,把解决经典问题的思路迁移过来解决新的问题。另一种方法是先问一个简单地问题 ,在应聘者答完简单地问题后,再追问一个相关的同时难度也更大的问题 。这时候面试官希望应聘者能够总结前面解决简单问题的经验,把前面的思路、方法迁移过来。
知识迁移能力的一种通俗的说法是“举一反三”的能力 。面试题是刷不完的 ,不可能把所有的面试题都准备一遍,因此更重要的是每做一道面试题的时候,都要总结这道题的解法有什么特点,有哪些思路是可以应用到同类型的题目中去的。
面试题53-59 面试题53:在排序数组中查找数字。
题目一:数字在排序数组中出现的次数。
统计一个数字在排序数组中出现的次数,例如,输入排序数组{1,2,3,3,3,3,4,5}和3,由于3在这个数组中出现了4次,因此输出4。
最普通的遍历法时间复杂度O(n),所以优化方法的时间复杂度肯定要优于O(n)。可以考虑用二分法方式寻找该数字的第一个位置和最后一个位置,然后就可以计算出出现次数了。在二分法时,首先找到有这个数的区间,当mid为寻找的目标数时,如果是寻找第一个位置,则看其左边是不是同样的数,如果是则在左侧继续寻找第一个位置,如果不是则mid就是第一个位置,寻找最后一个位置原理类似。
完整实现代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 #include <iostream> int find_head (int * data, int start, int end, int target) if (start == end) { if (data[start] == target) { return start; } else { return -1 ; } } int mid = (start + end) / 2 ; if (data[mid] == target) { if (mid == 0 || data[mid-1 ] != target) { return mid; } else { return find_head(data, start, mid-1 , target); } } else if (data[mid] < target) { return find_head(data, mid+1 , end, target); } else { return find_head(data, start, mid-1 , target); } } int find_tail (int * data, int start, int end, int target) if (start == end) { if (data[start] == target) { return start; } else { return -1 ; } } int mid = (start + end) / 2 ; if (data[mid] == target) { if (mid == end || data[mid+1 ] != target) { return mid; } else { return find_tail(data, mid+1 , end, target); } } else if (data[mid] < target) { return find_tail(data, mid+1 , end, target); } else { return find_tail(data, start, mid-1 , target); } } int counts_in_order (int * data, int len, int target) if (data == nullptr || len <= 0 ) { return 0 ; } int head = find_head(data, 0 , len-1 , target); int tail = find_tail(data, 0 , len-1 , target); if (head == -1 || tail == -1 ) { return 0 ; } else { return tail - head + 1 ; } } int main () int data[] = {1 ,2 ,3 ,3 ,3 ,3 ,4 ,5 }; printf ("Count:%d\n" , counts_in_order(data, 8 , 3 )); return 0 ; }
代码中,find_head、find_tail都是二分查找算法在数组中查找数字,时间复杂度都是O(logn),因此总的时间复杂度也是O(logn)。
题目二:0~n-1中缺失的数字。
一个长度n-1的递增排序数组中,所有数字都是唯一的,并且每个数字都在范围0~n-1中,在范围0~n-1内的n个数字中有且只有一个数字不在数组中 ,请找出这个数字。
最简单的方法是遍历数组求和,用0~n-1的总和n(n-1)/2相减就可以得到缺失的数字,但时间复杂度O(n),可以观察n-1长度的数组,如果缺失了第i个数,由于排序的性质,对任意的i<j第j个数会在j-1位置上,即不满足j在第j个位置上,所以问题转换为,找出第一个值和下标不相等的元素,利用二分法查找即可。
完整实现代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 #include <iostream> int find_miss_num (int * data, int start, int end) if (start == end) { if (data[start] != start) { return start; } else { return -1 ; } } int mid = (start + end) / 2 ; if (data[mid] != mid) { if (mid == start || data[mid-1 ] == mid-1 ) { return mid; } else { return find_miss_num(data, start, mid - 1 ); } } else { return find_miss_num(data, mid + 1 , end); } } int find_miss_num (int * data, int len) if (data == nullptr || len <= 0 ) { return -1 ; } return find_miss_num(data, 0 , len-1 ); } int main () int data[] = {0 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 }; printf ("Miss is %d\n" , find_miss_num(data, 9 )); return 0 ; }
题目三:数组中数值和下标相等的元素。
假设一个单调递增的数组 里的每个元素都是整数并且唯一 。请实现一个函数,找出数组中任意一个 数值等于其下标的元素。例如,在数组{-3,-1,1,3,5}中,数字3和它的下标相等。
以{-3,-1,1,3,5}和{0,1,2,3,4}为例来分析,可以发现规律,3的左边都是value < index,3的右边都是value > index,根据这一点来判断二分查找的下一个位置。
完整实现代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 #include <iostream> int find_index_eq_value (int * data, int start, int end) if (start == end) { if (data[start] == start) { return start; } else { return -1 ; } } int mid = (start + end) / 2 ; if (data[mid] == mid) { return mid; } else if (data[mid] < mid) { return find_index_eq_value(data, mid + 1 , end); } else { return find_index_eq_value(data, start, mid - 1 ); } } int find_index_eq_value (int * data, int len) if (data == nullptr || len <= 0 ) { return -1 ; } return find_index_eq_value(data, 0 , len-1 ); } int main () int data[] = {-3 , -1 , 1 , 3 , 5 }; printf ("Result: %d\n" , find_index_eq_value(data, 5 )); return 0 ; }
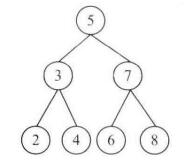
面试题54:二叉搜索树的第K大节点。
给定一棵二叉搜索树,请找出其中第K大的节点 。例如在下图中的二叉搜索树,按节点数值大小顺序,第3大节点的值是4。
书上的方法是直接简单的用二叉搜索树的性质,中序遍历即树中节点的递增排序,在中序遍历中找到第K大的节点。
完整实现代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 #include <iostream> struct node { int value; node* pleft; node* pright; }; node* init_node (int value) { ... }node* init_tree () { ... }node* find_kth_in_tree_core (node* proot, unsigned int & k) { node* target = nullptr ; if (proot->pleft != nullptr ) { target = find_kth_in_tree_core(proot->pleft, k); } if (target == nullptr ) { if (k == 1 ) { target = proot; } k--; } if (target == nullptr && proot->pright != nullptr ) { target = find_kth_in_tree_core(proot->pright, k); } return target; } node* find_kth_in_tree (node* proot, unsigned int k) { if (proot == nullptr || k == 0 ) { return nullptr ; } return find_kth_in_tree_core(proot, k); } int main () node* proot = init_tree(); printf ("%dth node is: %d" , 3 , find_kth_in_tree(proot, 3 )->value); return 0 ; }
面试题55:二叉树的深度。
题目一:二叉树的深度。
输入一棵二叉树的根节点,求该树的深度。从根节点到叶节点一次经过的节点(含根、叶节点)形成树的一条路径,最长路径的长度为树的深度 。
节点定义如下:
1 2 3 4 5 struct node { int value; node* pleft; node* pright; };
思路比较简单,就是节点的深度等于左右子树的最大深度+1 ,递归地实现即可。
完整实现代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 #include <iostream> struct node { int value; node* pleft; node* pright; }; node* init_node (int value) { ... }node* init_tree () { ... }int tree_depth (node* proot) if (proot == nullptr ) { return 0 ; } int left_depth = tree_depth(proot->pleft); int right_depth = tree_depth(proot->pright); return (left_depth > right_depth) ? (left_depth + 1 ) : (right_depth + 1 ); } int main () node* proot = init_tree(); printf ("Tree depth:%d\n" , tree_depth(proot)); return 0 ; }
题目二:平衡二叉树。
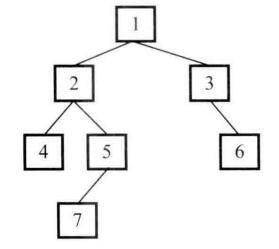
输入一棵二叉树的根节点,判断该树是不是平衡二叉树 。如果某二叉树中任意节点的左、右子树的深度相差不超过1,那么它就是一棵平衡二叉树。例如,下图就是一颗平衡二叉树。
在题目一的基础上,在每个节点上一边判断是否平衡,同时一边返回他们的深度,如果是先检查深度,再去检查子树是否平衡,就会频繁多次的访问子节点,导致时间上的浪费。
完整实现代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 #include <iostream> struct node { int value; node* pleft; node* pright; }; node* init_node (int value) { ... }node* init_tree () { ... }bool is_balanced (node* proot, int * pdepth) if (proot == nullptr ) { *pdepth = 0 ; return true ; } int left, right; if (is_balanced(proot->pleft, &left) && is_balanced(proot->pright, &right)) { int diff = left - right; if (diff <= 1 && diff >= -1 ) { *pdepth = 1 + (left > right ? left : right); return true ; } } return false ; } bool is_balanced (node* proot) int depth = 0 ; return is_balanced(proot, &depth); } int main () node* proot = init_tree(); if (is_balanced(proot)) { printf ("Is Balanced.\n" ); } else { printf ("Is Not Balanced.\n" ); } return 0 ; }
面试题56:数组中数字出现的次数。
题目一 :数组中只出现一次的两个数字。
一个整型数组里除两个数字之外,其他数字都出现了两次 。请写程序找出这两个只出现一次 的数字。要求时间复杂度是O(n),空间复杂度是O(1)。
这个题常规思路很难解决,需要使用到两个相同的数的异或为0 这种知识点,首先把问题分解为在一个整数数组中,除了一个数字之外,其他都出现两次 的一个子问题,对于这个子问题的求解方式是对所有数进行异或操作,最后结果数就是出现一次的数字(其中使用到了异或操作的交换律以及结合律,这里不再证明)。
再回到原始问题,看看有没有相同的思路。还是从头到尾异或每个数字,结果是两个只出现一次的数字的异或结果,因为其他数字都出现两次,在异或中全部抵消了。由于这两个数字不一样,所以异或的结果肯定不为0,至少有一位是1 (这代表这两个数,一个在该位上为1,一个在该位上为0),我们在结果数字中找到第一个为1的位的位置,记为第n位。现在我们以第n位是不是1位标准把原数组中的数字分为两个子数组 ,第一个子数组中每个数字的第n位都是1,第二个子数组中每个数字的第n位都是0,这样两个不同的数字就分到了两个数组中,并且相同的数字一定会被分到一个数组中,也就拆分成了两个可以解决的子问题了 。
完整实现代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 #include <iostream> unsigned int find_first_1_bit (int num) int index = 0 ; while ((num & 1 ) == 0 && index < 8 * sizeof (int )) { num = num >> 1 ; index++; } return index; } bool is_bit_1 (int num, unsigned int index) num = num >> index; return (num & 1 ); } bool g_invalid_input = false ;void find_nums_appear_once (int data[], int len, int * num1, int * num2) g_invalid_input = false ; if (data == nullptr || len < 2 || len % 2 != 0 ) { g_invalid_input = true ; return ; } int xor_result = 0 ; for (int i = 0 ; i < len; i++) { xor_result ^= data[i]; } unsigned int index_of_1 = find_first_1_bit(xor_result); *num1 = *num2 = 0 ; for (int i = 0 ; i < len; i++) { if (is_bit_1(data[i], index_of_1)) { *num1 ^= data[i]; } else { *num2 ^= data[i]; } } } int main () int data[] = {1 , 1 , 2 , 2 , 3 , 4 , 4 , 5 , 5 , 3 }; int num1 = 0 , num2 = 0 ; find_nums_appear_once(data, 10 , &num1, &num2); if (g_invalid_input) { printf ("Error: Invalid Input.\n" ); } else { printf ("Num1: %d, Num2: %d\n" , num1, num2); } return 0 ; }
题目二 :数组中唯一只出现一次的数字。
在一个数组中除一个数字只出现一次之外 ,其他数字都出现了三次 。请找出那个只出现一次的数字。
如果一个数字出现三次,那么它的二进制表示的每一位(0或者1)也出现3次 ,如果把所有出现三次的数字的二进制表示的每一位分别都加起来,那么每一位的和都能被3整除。这样我们把数组中所有数字的二进制表示的每一位都加起来。如果某一位的和能被3整除,那么那个只出现一次的数字的二进制表示中对应的那一位就是0,否则是1。
完整实现代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 #include <iostream> bool g_invalid_input = false ;int find_num_appear_once (int data[], int len) g_invalid_input = false ; if (data == nullptr || len <= 0 || len % 3 != 1 ) { g_invalid_input = true ; return 0 ; } int bit_sum[32 ] = { 0 }; for (int i = 0 ; i < len; i++) { int bit_mask = 1 ; for (int j = 31 ; j >= 0 ; j--) { int bit = data[i] & bit_mask; if (bit != 0 ) { bit_sum[j]++; } bit_mask = bit_mask << 1 ; } } int result = 0 ; for (int i = 0 ; i < 32 ; ++i) { result = result << 1 ; result += bit_sum[i] % 3 ; } return result; } int main () int data[] = {1 , 1 , 1 , -2 , -2 , -2 , -100 , 4 , 4 , 4 , 5 , 5 , 5 }; int result = find_num_appear_once(data, 13 ); if (g_invalid_input) { printf ("Error: Invalid Input.\n" ); } else { printf ("Result: %d\n" , result); } return 0 ; }
这种方法同样只需要O(n)的时间以及O(1)的空间,相比于其他方法有更好的时间效率(例如用排序需要O(logn)),同时也不会有多余的空间开销(例如用哈希表,需要额外的O(n)空间)。
面试题57:和为s的数字。
题目一:和为s的两个数字。
输入一个递增排序 的数组和一个数字s,在数组中查找两个数 ,使得它们的和正好是s。如果有多对数字的和 等于s,则输出任意一对即可。
PS:在面试的时候,很重要的一点是应聘者要表现出很快的反应能力。只要想到一种方法,应聘者就可以马上告诉面试官(仅限于面谈形式的),即使这种方法不一定是最好的。
根据已排序数组的特性,当指定数组中的两个数字时:
如果两个数字的和小于s,需要一个更大的数字,这个时候可以在较小数字的右侧** 或者是较大数字的 右侧**去寻找; 如果两个数字的和大于s,需要一个更小的数字,这个时候可以在较小数字的左侧** 或者是较大数字的 左侧**去寻找; 如果两个数字的和等于s,则找到两个满足要求的数字。 仅仅分析到这里是还不够的,如果每个位置都要考虑两种情况,最后的复杂度会是O(2^n),在这种去情况时,可以考虑固定一个方向寻找,并且要能够覆盖到所有情况,例如本题中,可以初始化一头一尾两个指针,如果和小于s,移动头指针向右,如果和大于s,移动头指针向左,这样可以遍历到所有情况 。
PS:为什么说这样可以遍历到所有情况? 对于每一个头指针指向的数字,你不能在当前尾指针的右侧找到一个更适合的数(都是大于s);对于每一个尾指针指向的数字,你不能在当前头指针的左侧找到一个更适合的数(都是小于s),所以这样逐步缩小范围,同时也考虑到了所有情况。
完整实现代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 #include <iostream> int g_invalid_input = false ;int find_nums_with_sum (int data[], int len, int sum, int * num1, int * num2) g_invalid_input = false ; bool found = false ; if (data == nullptr || len < 2 || !num1 || !num2) { g_invalid_input = true ; return found; } int head = 0 ; int tail = len - 1 ; while (head < tail) { long long cur_sum = data[head] + data[tail]; if (cur_sum == sum) { *num1 = data[head]; *num2 = data[tail]; found = true ; break ; } else if (cur_sum > sum) { tail--; } else { head++; } } return found; } int main () int data[] = {1 , 2 , 4 , 7 , 11 , 15 }; int num1, num2; if (find_nums_with_sum(data, 6 , 15 , &num1, &num2)) { printf ("Found! Num1: %d, Num2: %d\n" , num1, num2); } else if (g_invalid_input) { printf ("Error: Invalid Input.\n" ); } else { printf ("Not Found!\n" ); } return 0 ; }
题目二 :和为s的连续正数序列。
输入一个正数s,打印出所有和为s的连续正数序列 (至少含有两个数)。例如,输入15,由于1+2+3+4+5=4+5+6+7=7+8=15,所以打印出3个连续序列1~5、4~6、7~8。
和题目一思路类似。
完整实现代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 #include <iostream> void find_seqs_with_sum (int sum) if (sum <= 0 ) { return ; } int head = 1 ; int tail = 2 ; int cur_sum = head + tail; while (!(head == tail - 1 && cur_sum > sum)) { if (cur_sum == sum) { printf ("%d~%d\n" , head, tail); cur_sum -= head; head++; } else if (cur_sum > sum) { cur_sum -= head; head++; } else { tail++; cur_sum += tail; } } } int main () find_seqs_with_sum(15 ); return 0 ; }
面试题58:翻转字符串。
题目一 :翻转单词顺序。
输入一个英语句子,翻转句子中单词的顺序,但单词内字符的顺序不变。简单起见,标点符号和字幕一样处理。例如输入I am a student.,则输出student. a am I.
普通方法的思路也不是特别难,不过这里说一下书上的两次翻转字符串的解法:
第一步翻转句子中所有的字符 ; 第二步翻转每个单词中的字符的顺序 ,就得到了最终结果。 完整实现代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 #include <iostream> void reverse (char * pstart, char * pend) if (pstart == nullptr || pend == nullptr ) { return ; } while (pstart < pend) { char temp = *pstart; *pstart = *pend; *pend = temp; pstart++; pend--; } } void str_reverse (char * str) if (str == nullptr ) { return ; } char * pstart = str; char * pend = str; while (*pend != '\0' ) { pend++; } pend--; reverse(pstart, pend); pstart = pend = str; while (*pstart != '\0' ) { if (*pstart == ' ' ) { pstart++; pend++; } else if (*pend == ' ' || *pend == '\0' ) { reverse(pstart, pend - 1 ); pstart = pend; } else { pend++; } } } int main () char str[] = " I am a student. " ; str_reverse(str); if (str != nullptr ) { printf ("%s" , str); } return 0 ; }
题目二 :左旋转字符串。
字符串的左旋转操作是把字符串前面的若干个字符 转移到字符串的尾部 。比如输入字符串abcdefg和数字2,函数返回左旋两位得到的结果cdefgab。
题目一中的翻转字符串,如果在本例中,可以类比于将ab cdefg翻转为cdefg ab,所以可以使用和题目一类似的思路。
完整实现代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 #include <iostream> #include <cstring> void reverse (char * pstart, char * pend) if (pstart == nullptr || pend == nullptr ) { return ; } while (pstart < pend) { char temp = *pstart; *pstart = *pend; *pend = temp; pstart++; pend--; } } void str_left_rotate (char * str, int n) int len = strlen (str); if (str == nullptr || n < 0 || n >= len || len == 0 ) { return ; } char * pstart; char * pend; pstart = str; pend = str + n - 1 ; reverse(pstart, pend); pstart = str + n; pend = str + len - 1 ; reverse(pstart, pend); pstart = str; pend = str + len - 1 ; reverse(pstart, pend); } int main () char str[] = "abcdefg" ; str_left_rotate(str, 2 ); if (str != nullptr ) { printf ("%s" , str); } }
面试题59:队列的最大值。
题目一 :滑动窗口的最大值。
给定一个数组和滑动窗口大小,请找出所有滑动窗口里的最大值。例如{2,3,4,2,6,2,5,1}以及滑动窗口大小3,那么一共存在6个滑动窗口,他们的最大值分别是{4,4,6,6,6,5}。
使用一个双端队列来保存当前窗口最大值以及可能的次最大值们 ;如果新入窗口的元素大于队列的头元素(最大值),则清空队列,头部入队新元素;如果新入窗口的元素小于队列的头元素,则出尾部所有小于该新元素的数字,并在尾部入队新元素;同时在队列中只需要保存元素的index,用来同时获取数字以及判断当前其是否在窗口内,如果不在窗口内就要进行出队。
完整实现代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 #include <iostream> #include <deque> #include <vector> using namespace std ;vector <int > windows_max (const vector <int >& num, unsigned int size) vector <int > maxs; if (num.size() < size && size >= 1 ) { return maxs; } deque <int > index; for (unsigned int i = 0 ; i < size; i++) { while (!index.empty() && num[i] >= num[index.back()]) { index.pop_back(); } index.push_back(i); } for (unsigned int i = size; i < num.size(); i++) { maxs.push_back(num[index.front()]); while (!index.empty() && num[i] >= num[index.back()]) { index.pop_back(); } if (!index.empty() && index.front() <= (int )(i - size)) { index.pop_front(); } index.push_back(i); } maxs.push_back(num[index.front()]); return maxs; } int main () vector <int > num ({2 ,3 ,4 ,2 ,6 ,2 ,5 ,1 }) vector <int > maxs = windows_max(num, 3 ); for (int i = 0 ; i < maxs.size(); i++) { printf ("%d " , maxs[i]); } return 0 ; }
题目二 :队列的最大值。
定义一个队列,并实现函数max得到队列里的最大值,要求函数max、push_back和pop_front的时间复杂度都是O(1)。
思路和题目一类似,使用一个双端队列实现max。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 #include <iostream> #include <deque> using namespace std ;template <typename T> class QueueWithMAx { public : QueueWithMAx(): cur_index(0 ) {} void push_back (T num) while (!maxs.empty() && num >= maxs.back().num) { maxs.pop_back(); } InternalData idata = { num, cur_index }; data.push_back(idata); maxs.push_back(idata); cur_index++; } void pop_front () if (maxs.empty()) { printf ("Error: queue is empty\n" ); } if (maxs.front().index == data.front().index) { maxs.pop_front(); } data.pop_front(); } int front () if (data.empty()) { printf ("Error: queue is empty\n" ); } return data.front().num; } T max () const { if (maxs.empty()) { printf ("Error: queue is empty\n" ); } return maxs.front().num; } private : struct InternalData { T num; int index; }; deque <InternalData> data; deque <InternalData> maxs; int cur_index; }; int main () int num[] = {2 ,3 ,4 ,2 ,6 ,2 ,5 ,1 }; QueueWithMAx<int > queue ; for (int i = 0 ; i < 8 ; i++) { queue .push_back(num[i]); printf ("After push %d, max is %d\n" , num[i], queue .max()); } for (int i = 0 ; i < 7 ; i++) { int front = queue .front(); queue .pop_front(); printf ("After pop %d, max is %d\n" , front, queue .max()); } return 0 ; }
4 抽象建模能力 有些面试官喜欢从日常生活中抽取提炼出问题,考查应聘者是否能简历数学模型并解决问题。
建模的第一步是选择合理的数据结构来表述问题 。我们在根据问题的特点,综合考虑性能、编程难度等因素之后,选择最合适的数据结构来表达问题,也就是建立模型。
建模的第二步是分析模型中的内在规律,并用编程语言表述这种规律 。
面试题60-63 面试题60:n个骰子的点数。
把n个骰子扔在地上,所有骰子朝上一面的点数之和为s。输入n,打印出现s的所有可能的值出现的概率。
最简单的方法递归地遍历骰子的所有值情况,然后记录和s的出现次数,时间复杂度O(6^n),当n很大时难以接受。
其实可以简化这个问题,例如设f(n,s)为n个骰子时和s的出现次数,则有f(n,s)=f(n-1,s-1)+f(n-1,s-2)+f(n-1,s-3)+f(n-1,s-4)+f(n-1,s-5)+f(n-1,s-6),写出这样的递归式,我们就可以想到通过迭代来代替递归的方式计算结果,设初值f(1,k)=1, 1<=k<=6,每次迭代,向后计算即可,时间复杂度O(n^2)。
完整实现代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 #include <iostream> #include <algorithm> #include <cmath> void print_probability (int n) if (n < 1 ) { return ; } int size = 6 * n + 1 ; int * prob1 = new int [size]; int * prob2 = new int [size]; std ::fill(prob1, prob1 + size, 0 ); std ::fill(prob2, prob2 + size, 0 ); std ::fill(prob1 + 1 , prob1 + 7 , 1 ); for (int i = 0 ; i < n - 1 ; i++) { for (int j = 1 ; j < size; j++) { prob2[j] = 0 ; for (int k = 1 ; k <= 6 && j-k>=0 ; k++) { prob2[j] += prob1[j-k]; } } int * temp = prob1; prob1 = prob2; prob2 = temp; } double total = (double )std ::pow (6 , n); for (int i = n; i < size; i++) { printf ("%d: %d\n" , i, prob1[i]); } delete [] prob1; delete [] prob2; } int main () print_probability(11 ); return 0 ; }
相比于书上的代码,这一版本更加简洁。
面试题61:扑克牌中的顺子。
从扑克牌中随机抽5张牌,判断是不是一个顺子,即这5张牌是不是连续的。2~10为数字,A为1、J为11、Q为12、K为13,而大、小王可以看成任意数字 。
思路比较基础,就是先把手里的数组排序(大小王当作0),统计0的个数,统计排序相邻数字之间的空缺总数,如果综述小于等于0的个数,则数组连续,否则不连续。如果数组中非0数字重复出现,则该数字不是连续的。
完整实现代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 #include <iostream> #include <algorithm> bool is_straight (int * numbers, int len) if (numbers == nullptr || len < 1 ) { return false ; } std ::sort(numbers, numbers+len); int zeros = 0 ; int gaps = 0 ; for (int i = 0 ; i < len; i++) { if (numbers[i] == 0 ) { zeros++; continue ; } if (i > 0 && numbers[i] == numbers[i-1 ]) { return false ; } if (i > 0 ) { gaps += numbers[i] - numbers[i-1 ] - 1 ; } } if (gaps <= zeros) { return true ; } else { return false ; } } int main () int nums[] = {1 , 2 , 0 , 4 , 5 }; if (is_straight(nums, sizeof (nums)/sizeof (int ))) { printf ("Is straight." ); } else { printf ("Is not straight." ); } return 0 ; }
如果觉得代码中排序的部分O(nlogn)不够快,因为这里出现的数字只有0~13,所以还可以使用哈希表实现O(n)的排序。
面试题62:圆圈中最后剩下的数字。
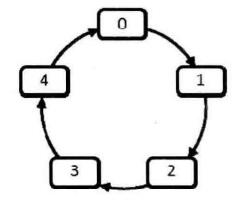
0,1,...,n-1这n个数字排成一个圆圈,从数字0开始,每次从这个圆圈里删除第m个数字。求出这个圆圈里剩下的最后一个数字。
例如上图的圆圈,从数字0开始,每次删除第3个数字,则删除的前4个数字是2、0、4、1,最后剩下的数字是3。
本题就是有名的约瑟夫(Josephuse)环问题。一种方法是用环形链表模拟圆圈的经典解法,时间复杂度O(nm),另一种方法是分析被删除数字的规律,直接计算出圆圈中最后剩下的数字,时间复杂度O(n)。
链表模拟法就不再赘述了,主要讲一下第二个的规律分析法。
定义一个关于n和m的函数f(n,m),表示每次在n个数字0,1,...,n-1中删除第m个数字最后剩下的数字。
在这n个数字中,第一个被删除的是(m-1)%n,简单起见,记为k,删除k之后剩下的n-1个数字为0,1,...,k-1,k+1,...,n-1,并且在下一次删除从数字k+1开始计数。相当于在剩下的序列中,k+1排在最前面,从而形成k+1,...,n-1,0,1,...,k-1。这个序列最后剩下的数字应该也是关于n和m的函数。
由于第二个序列和前面最初的序列不一样,因此函数不同于前面的函数,记为f'(n-1,m),所以有f(n,m)=f'(n-1,m)。
接下来我们把,剩下的这n-1个数字的序列k+1,...,n-1,0,1,...,k-1进行映射,结果形成一个0~n-2的序列。
把映射定义为p,则有p(x)=(x-k-1)%n,映射的逆映射是p'(x)=(x+k+1)%n。
由于映射之后的序列和最初的序列具有相同的形式,即都是从0开始的连续序列,因此仍然可以用函数f来表示,记为f(n-1,m)。根据我们之前的推导,映射之前的序列剩下的数字是f'(n-1,m)=p'(f(n-1,m))=(f(n-1,m)+k+1)%n,把k=(m-1)%n代入,可以得到f(n,m)=f'(n-1,m)=[f(n-1,m)+m]%n。
通过分析后,我们找到了一个递归公式,要得到这n个数的序列中最后剩下的数字,只需要得到n-1个数字的序列中最后剩下的数字,并以此类推。
当n=1时,序列中只有一个数字0,那么很显然最后剩下的数字就是0,这种递归可以写为:
公式无论是用递归还是循环,都很容易实现。
完整实现代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 #include <iostream> int last_remaining (unsigned int n, unsigned int m) if (n < 1 || m < 1 ) { return -1 ; } int last = 0 ; for (int i = 2 ; i <= n; i++) { last = (last + m) % i; } return last; } int main () printf ("%d" , last_remaining(5 , 3 )); return 0 ; }
时间复杂度O(n),空间复杂度O(1)。
面试题63:股票的最大利润。
假设把某股票的价格按照时间先后顺序存储在数组中,请问买卖该股票一次,可能获得的最大利润 是多少?例如一支股票在某些时间节点的价格为{9,11,8,5,7,12,16,14}。如果我们能在价格5时买入,并在价格16时卖出,则收获最大利润11。
暴力遍历法时间复杂度O(n^2),但是只要在从前向后计算的时候,保存前面序列中的最小值,就可以计算出当前值和前面序列的最小值的差值,最后获得最大差值就是最大利润。
完整实现代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 #include <iostream> #include <limits.h> int max_profit (int * numbers, int len) if (numbers == nullptr || len < 2 ) { return 0 ; } int min = numbers[0 ]; int max_profits = INT_MIN; for (int i = 1 ; i < len; i++) { if (numbers[i] - min > max_profits) { max_profits = numbers[i] - min; } if (min > numbers[i]) { min = numbers[i]; } } return max_profits; } int main () int numbers[] = {9 ,11 ,8 ,5 ,7 ,12 ,16 ,14 }; printf ("max profit is %d" , max_profit(numbers, sizeof (numbers)/sizeof (int ))); return 0 ; }
只需要扫描数组一次,该算法的时间复杂度O(n)。
5 发散思维能力 发散思维的特点是思维活动的多向性和变通性,也就是思考问题时,注重运动多思路、多方案、多途径来解决问题。对于同一个问题,我们可以从不同的方向、侧面和层次,采用探索、转移、迁移、组合和分解等方法,提出多种创新的解法。
面试题64-66 面试题64:求1+2+…+n。
求1+2+...+n,要求不能使用乘除法、for、while、if、else、switch、case等关键字及条件判断语句(A?B:C)。
循环和递归实现在本题中就没办法使用了,可以尝试从一些语言特性的方面来解决。
解法一 :利用构造函数求解。
循环只是让相同的代码重复执行n次而已,完全可以不用for和while来达到这个效果。比如定义一个类型,接着创建n个该类型的实例,那么这个类型的构造函数将确定会被调用n次,可以将与累加相关的代码放到构造函数里。
完整实现代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 #include <iostream> class Temp {public : Temp() { ++N; Sum+=N; } static void reset () N = 0 ; Sum = 0 ; } static unsigned int get_sum () return Sum; } private : static unsigned int N; static unsigned int Sum; }; unsigned int Temp::N = 0 ;unsigned int Temp::Sum = 0 ;unsigned int sum_solution1 (unsigned int n) Temp::reset(); Temp* a = new Temp[n]; delete [] a; a = nullptr ; return Temp::get_sum(); } int main () printf ("%d" , sum_solution1(10 )); return 0 ; }
解法二 :利用虚函数求解。
同样可以围绕递归来做,既然不能在一个函数中判断是不是应该终止递归,那么不妨定义两个函数,一个充当递归函数,另一个函数处理终止递归地情况,需要做的就是在两个函数里二选一,从二选一我们很自然地想到布尔变量,比如值为true时,调用第一个函数,值为false时,调用第二个函数。
完整实现代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 #include <iostream> class A ;A* Array[2 ]; class A {public : virtual unsigned int sum (unsigned int n) return 0 ; } }; class B :public A {public : virtual unsigned int sum (unsigned int n) return Array[(bool )n]->sum(n-1 )+n; } }; int sum_solution2 (int n) A a; B b; Array[0 ] = &a; Array[1 ] = &b; int value = Array[1 ]->sum(n); return value; } int main () printf ("%d" , sum_solution2(10 )); return 0 ; }
使用虚函数来实现函数的选择,当n不为0时,调用函数B::sum,当n等于0时,调用函数A::sum。
解法三 :利用函数指针求解。
纯C语言的变成环境中,我们不能使用虚函数,此时可以用函数指针来模拟,这样代码可能还更加直观一点。
完整实现代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 #include <iostream> typedef unsigned int (*fun) (unsigned int ) unsigned int terminator (unsigned int n) return 0 ; } unsigned int sum_solution3 (unsigned int n) static fun f[2 ] = {terminator, sum_solution3}; return n + f[(bool )n](n-1 ); } int main () printf ("%d" , sum_solution3(10 )); return 0 ; }
解法四 :利用模板类求解。
还可以让编译器帮助完成类似于递归地计算。
完整能够代码实现:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 #include <iostream> template <unsigned int n> struct sum_solution4 { enum value {-1 >::N + n }; }; template <> struct sum_solution4 <1 > { enum Value {1 }; }; int main () printf ("%d" , sum_solution4<10 >::N); return 0 ; }
当编译器看到sum_solution4<10>,就会为模板类sum_solution4以参数10生成该类型的代码,并且以10为参数的类型需要得到以9为参数的类型,这个过程会一直递归到参数为1的类型(已经显式定义,编译器无须生成)。
由于这个过程是在编译过程中完成的,因此要求输入的n必须是在编译期间就能确定的常量,不能动态输入。而且编译器对递归编译代码的递归深度是有限制的,要求n不能太大。
面试题65:不用加减乘除做加法。
写一个函数,求两个整数之和,要求在函数体内不得使用+、-、×、÷四则运算符号。
不能用四则运算的话,就只能考虑用位运算(与、或、非、异或)的方式来实现加法了。
例如5+17=22,5的二进制是101,17的二进制是10001,我们试着把计算分成三步:
第一步,各位相加,不计进位,得到的结果是10100(1+1溢出后就是0); 第二步,记下进位,在这个例子中只在最后一位相加时产生一个进位,结果是二进制的10; 第三步,把前两步的结果相加,得到结果10110,转换成十进制就是22。 现在把二进制的加法用位运算来代替:
第一步,非进位加法,其实和异或运算相同,例如101^10001=10100; 第二步,只有1加1时,会向前产生一个进位1,此时我们可以想象成两个数先做位与运算,然后再向左移动一位,例如101&10001 << 1 = 10; 第三步,把前面两步结果相加,又变成一个新的问题,递归调用前两步,直到不会再产生进位为止。 完整实现代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 #include <iostream> bool same_sign (int num1, int num2) return (num1 >> 31 ) == (num2 >> 31 ); } int bit_add (int num1, int num2) int sum, carry; int tnum1 = num1, tnum2 = num2; do { sum = tnum1^tnum2; carry = (tnum1 & tnum2) << 1 ; tnum1 = sum; tnum2 = carry; } while (tnum2 != 0 ); if (same_sign(num1, num2) && !same_sign(num1, sum)) { printf ("Error: add overflow\n" ); return 0 ; } else { return sum; } } int main () printf ("%d" , bit_add(200 , 20 )); return 0 ; }
在书上的代码基础上,加入对溢出的异常判断,其中对于溢出判定方法是,只有当两个数同号时才会在加法中溢出,并且最后结果和原来的两个数异号时,就代表发生了溢出,此时应该抛出异常。
PS:不使用新的变量,交换两个变量的值(适用于数值类)。比如有a、b,我们希望交换它们的值。有两种不同的方法:
面试题66:构建乘积数组。
给定一个数组A[0,1,...,n-1],请构建一个数组B[0,1,...,n-1],其中B中的元素B[i]=A[0]*A[1]*...*A[i-1]*A[i+1]*...*A[n-1]。不能使用除法。
因为不能使用除法,所以只能另辟蹊径,如果用暴力求解法,时间复杂度是O(n)。
如果单独地求解A[0]*A[1]*...*A[i-1],我们是可以迭代地在O(n)时间里求解出所有的前序乘积的,同理所有的A[i-1]*A[i+1]*...*A[n-1],我们也可以逆序地迭代O(n)的时间中求解,最后对于每一个B[i]找到对应的前序序列和逆序序列就可以用乘法得到最后的结果了。
PS:不知道这道题要不要考虑什么乘积大数溢出的问题,根据面试的具体情况来分析吧,这种题再加上大数就稍微有点复杂了。
完整实现代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 #include <iostream> #include <vector> using namespace std ;void multi_array (const vector <double >& array1, vector <double >& array2) int len1 = array1.size(); int len2 = array2.size(); if (len1 != len2 || len2 <= 1 ) { return ; } double temp = 1 ; for (int i = 0 ; i < len1; i++) { array2[i] = temp; temp *= array1[i]; } temp = 1 ; for (int i = len2 - 1 ; i >= 0 ; i--) { array2[i] *= temp; temp *= array1[i]; } } int main () vector <double > array1 ({1 , 2 , 3 , 4 , 5 }) vector <double > array2 (5 ) multi_array(array1, array2); for (int i = 0 ; i < array2.size(); i++) { printf ("%e " , array2[i]); } return 0 ; }
这种思路的时间复杂度是O(n)。
6 总结 面试是我们展示自己综合素质的时候,除了扎实的编程能力,我们还需要表现自己的沟通能力和学习能力,以及知识迁移能力、抽象建模能力和发散思维能力等方面的综合实力。